题目内容
利用不等式求最值,下列运用错误的是( )
A、若x<-1,则2x-1+
| ||||
B、
| ||||
C、y=2x+
| ||||
D、已知ab>0,
|
考点:基本不等式
专题:不等式的解法及应用
分析:利用基本不等式即可判断出,特别注意等号成立的条件.
解答:
解:A.当x<-1,2x-1<-3,∴1-2x>3,∴2x-1+
=-(1-2x+
)≤-2
=-2,当且仅当1-2x=1,解得x=0>-1,因此等号不成立,故不正确;
B.
=
+
≥2
=2,当且仅当x=0时取等号,因此正确.
C.∵2x>0,∴y=2x+
≥2
=2,当且仅当x=0时取等号,因此正确.
D.∵ab>0,∴
+
≥2
=2,当且仅当b=a时取等号,因此正确.
综上可得:只有A不正确.
故选:A.
| 1 |
| 2x-1 |
| 1 |
| 1-2x |
(1-2x)•
|
B.
| x2+2 | ||
|
| x2+1 |
| 1 | ||
|
|
C.∵2x>0,∴y=2x+
| 1 |
| 2x |
2x•
|
D.∵ab>0,∴
| b |
| a |
| a |
| b |
|
综上可得:只有A不正确.
故选:A.
点评:本题考查了基本不等式的性质,注意“一正二定三相等”,属于基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
已知椭圆
+
=1上一点P到椭圆的一焦点的距离为3,则P到另一焦点的距离是( )
| x2 |
| 9 |
| y2 |
| 5 |
A、2
| ||
| B、2 | ||
| C、3 | ||
| D、6 |
已知a、b、m为正实数,则不等式
>
成立的条件是( )
| a+m |
| b+m |
| a |
| b |
| A、a<b | B、a>b |
| C、a≤b | D、a≥b |
已知cosα=-
,α∈(0,180°),则α的值是( )
| ||
| 2 |
| A、45° | B、125° |
| C、135° | D、145° |
已知平行四边形的3个顶点为A(a,b),B(-b,a),C(0,0),则它的第4个顶点D的坐标是( )
| A、(2a,b) |
| B、(a+b,b-a) |
| C、(a-b,a+b) |
| D、(a-b,b-a) |
已知i是虚数单位,(1+2i)z=i,则
=( )
. |
| z |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
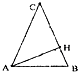 如图,在△ABC中,cos
如图,在△ABC中,cos