题目内容
已知f(
+1)=lgx,则f(21)= .
| 2 |
| x |
考点:函数解析式的求解及常用方法
专题:换元法,函数的性质及应用
分析:由题意,用换元法,设
+1=t,求出f(t),即可计算f(21)的值.
| 2 |
| x |
解答:
解:根据题意,设
+1=t(t>1),
则x=
,
∴f(t)=lg
,
即f(x)=lg
(x>1);
∴f(21)=lg
=-1.
故答案为:-1.
| 2 |
| x |
则x=
| 2 |
| t-1 |
∴f(t)=lg
| 2 |
| t-1 |
即f(x)=lg
| 2 |
| x-1 |
∴f(21)=lg
| 2 |
| 21-1 |
故答案为:-1.
点评:本题考查了用换元法求函数解析式的问题,解题时应先求出函数的解析式,再计算函数的值,是基础题.

练习册系列答案
相关题目
已知椭圆
+
=1上一点P到椭圆的一焦点的距离为3,则P到另一焦点的距离是( )
| x2 |
| 9 |
| y2 |
| 5 |
A、2
| ||
| B、2 | ||
| C、3 | ||
| D、6 |
已知平行四边形的3个顶点为A(a,b),B(-b,a),C(0,0),则它的第4个顶点D的坐标是( )
| A、(2a,b) |
| B、(a+b,b-a) |
| C、(a-b,a+b) |
| D、(a-b,b-a) |
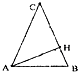 如图,在△ABC中,cos
如图,在△ABC中,cos