题目内容
15.已知函数f(x)=x|x|-mx+1有三个零点,则实数m的取值范围是( )| A. | (0,2) | B. | (2,+∞) | C. | (-∞,-2) | D. | [2,+∞) |
分析 f(x)=x|x|-mx+1得x|x|+1=mx利用参数分离法得m=|x|+$\frac{1}{x}$,构造函数g(x)=|x|+$\frac{1}{x}$,转化为两个函数的交点个数问题进行求解即可.
解答 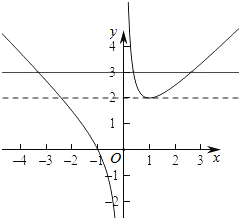 解:由f(x)=x|x|-mx+1得x|x|+1=mx,
解:由f(x)=x|x|-mx+1得x|x|+1=mx,
当x=0时,方程不成立,
即x≠0,
则方程等价为m=|x|+$\frac{1}{x}$
设g(x)=|x|+$\frac{1}{x}$,
当x<0时,g(x)=-x+$\frac{1}{x}$为减函数,
当x>0时,g(x)=x+$\frac{1}{x}$,
则g(x)在(0,1)上为减函数,则(1,+∞)上为增函数,
即当x=1时,函数取得极小值同时也是最小值g(1)=1+1=2,
作出函数g(x)的图象如图:
要使f(x)=x|x|-mx+1有三个零点,
则等价为m=|x|+$\frac{1}{x}$有三个不同的根,
即y=m与g(x)有三个不同的交点,则由图象知m>2,
故实数m的取值范围是(2,+∞),
故选:B.
点评 本题主要考查函数与方程的应用,利用参数分离法以及数形结合是解决本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
5.已知点A(2,0),B(0,-1),点P是圆x2+(y-1)2=1上的任意一点,则△PAB面积的最大值为( )
| A. | 2 | B. | $4+\sqrt{5}$ | C. | $1+\frac{{\sqrt{5}}}{2}$ | D. | $2+\frac{{\sqrt{5}}}{2}$ |
6.棱长为1的正四面体的外接球的半径为( )
| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{3}}}{4}$ | C. | 1 | D. | $\frac{{\sqrt{3}}}{3}$ |
10.已知函数f(x)=$\left\{\begin{array}{l}{{a}^{x}-1,x≤0}\\{f(x-1)+1,x>0}\end{array}\right.$(a>0,a≠1),把函数g(x)=f(x)-x的零点按照从小到大的顺序排成一个数列{an},则a2016的值为( )
| A. | 1008 | B. | 2015 | C. | 2016 | D. | 4032 |
20.设定义域为(0,+∞)的单调函数f(x),对任意的x∈(0,+∞),都有f[f(x)-lnx]=1,若函数y=x(f(x)-2)+b有零点,则实数b的取值范围是( )
| A. | (0,1) | B. | (-∞,1] | C. | (2,3) | D. | [2,+∞) |