题目内容
10.对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出定义:设f″是f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.有同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.请你根据这一发现为条件,若给定函数g(x)=$\frac{1}{3}{x^3}-\frac{1}{2}{x^2}+2x-\frac{5}{12}$,则g($\frac{1}{2017}$)+g($\frac{2}{2017}$)+g($\frac{3}{2017}$)+…+g($\frac{2016}{2017}$)=1008.分析 由题意对已知函数求两次导数可得图象关于点($\frac{1}{2}$,$\frac{1}{2}$)对称,即f(x)+f(1-x)=1,即可得到结论.
解答 解:函数的导数g′(x)=x2-x+2,
g″(x)=2x-1,
由g″(x0)=0得2x0-1=0
解得x0=$\frac{1}{2}$,而g($\frac{1}{2}$)=$\frac{1}{2}$,
故函数g(x)关于点($\frac{1}{2}$,$\frac{1}{2}$)对称,
∴g(x)+g(1-x)=1,
故设g($\frac{1}{2017}$)+g($\frac{2}{2017}$)+g($\frac{3}{2017}$)+…+g($\frac{2016}{2017}$)=m,
则g($\frac{2016}{2017}$)+g($\frac{2015}{2017}$)+…g($\frac{1}{2017}$)=m,
两式相加得1×2016=2m,
则m=1008,
故答案为:1008
点评 本题主要考查导数的基本运算,利用条件求出函数的对称中心是解决本题的关键.求和的过程中使用了倒序相加法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.设函数f(x)=x3+3x2+6x+14且f(a)=1,f(b)=19.则a+b=( )
| A. | 2 | B. | 1 | C. | 0 | D. | -2 |
2.设点P在面积为2的正△ABC内部运动,若动点P使得△PBC,△PAB,△PAC的面积都不大于1,则动点P的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
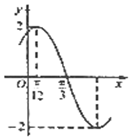 已知函数$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,下列说法正确的有( )个
已知函数$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,下列说法正确的有( )个