��Ŀ����
1��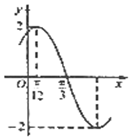 ��֪����$f��x��=Asin����x+ϕ����A��0���أ�0��|ϕ|��\frac{��}{2}��$�IJ���ͼ����ͼ��ʾ������˵����ȷ���У���������
��֪����$f��x��=Asin����x+ϕ����A��0���أ�0��|ϕ|��\frac{��}{2}��$�IJ���ͼ����ͼ��ʾ������˵����ȷ���У����������ٺ���f��x����ͼ�����ֱ��$x=-\frac{5��}{12}$�Գ�
�ں���f��x����$[-\frac{��}{3}��0]$�ϵ�������
�ۺ���f��x����ͼ����ڵ�$��-\frac{2��}{3}��0��$�Գ�
�ܽ�����y=2sin2x��ͼ������ƽ��$\frac{��}{3}$����λ�õ�f��x����ͼ��
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
���� ���ݺ���f��x���IJ���ͼ�����f��x���Ľ���ʽ���ٸ������Ǻ�����ͼ�������ʣ��ж���Ŀ�е������Ƿ���ȷ��
��� �⣺���ݺ���f��x���IJ���ͼ��֪��
A=2��$\frac{T}{4}$=$\frac{��}{3}$-$\frac{��}{12}$=$\frac{��}{4}$��
��T=����=$\frac{2��}{T}$=2��
����㷨��ͼ֪��x=$\frac{��}{12}$ʱf��$\frac{��}{12}$��=2��
��2��$\frac{��}{12}$+��=$\frac{��}{2}$����æ�=$\frac{��}{3}$��
��f��x��=2sin��2x+$\frac{��}{3}$����
���ڢ٣�x=-$\frac{5��}{12}$f��-$\frac{5��}{12}$��=2sin��2����-$\frac{5��}{12}$��+$\frac{��}{3}$��=-2
�ຯ��f��x����ͼ�����ֱ��$x=-\frac{5��}{12}$�Գƣ�������ȷ��
���ڢڣ�x��$[-\frac{��}{3}��0]$ʱ��2x+$\frac{��}{3}$��[-$\frac{��}{3}$��$\frac{��}{3}$]��f��x���ǵ�������������������ȷ��
���ڢۣ�x=-$\frac{2��}{3}$f��-$\frac{2��}{3}$��=2sin[2����-$\frac{2��}{3}$��+$\frac{��}{3}$]=0��
�ຯ��f��x����ͼ����ڵ�$��-\frac{2��}{3}��0��$�Գƣ�������ȷ��
���ڢܣ�������y=2sin2x��ͼ������ƽ��$\frac{��}{3}$����λ��
�õ�y=2sin2��x+$\frac{��}{3}$��=2sin��2x+$\frac{2��}{3}$����ͼ��
����f��x����ͼ���������
���ϣ���ȷ����������Ǣ٢ڢۣ���3����
��ѡ��C��
���� ���⿼�������Ǻ�����ͼ�������ʵ�Ӧ�����⣬Ҳ�������ɺ����IJ���ͼ�������ʽ��Ӧ�����⣬���ۺ��⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| A�� | a��b��c | B�� | b��a��c | C�� | c��b��a | D�� | c��a��b |
| A�� | ��0��1] | B�� | [-1��0�� | C�� | 0 | D�� | ��ȷ�� |