题目内容
5．已知动点M（x，y）的坐标满足$\sqrt{{{（x-2）}^2}+{y^2}}$=|x+2|，则动点M的轨迹是（ ）| A． | 椭圆 | B． | 双曲线 | C． | 抛物线 | D． | 以上均不对 |
分析 直接把已知等式两边平方化简得答案．
解答 解：由$\sqrt{{{（x-2）}^2}+{y^2}}$=|x+2|，两边平方得x2-4x+4+y2=x2+4x+4，
整理得：y2=8x，
∴动点M的轨迹是抛物线．
故选：C．
点评 本题考查轨迹方程，考查抛物线的标准方程，是基础题．
练习册系列答案
相关题目
15．已知$\frac{sinα-2cosα}{3sinα+5cosα}$=5，那么tanα的值为（ ）
| A． | -2 | B． | 2 | C． | -$\frac{27}{14}$ | D． | -$\frac{23}{16}$ |
16．已知全集U=R，A={x|x2-5x+6≥0}，则∁UA=（ ）
| A． | {x|x＞2} | B． | {x|x＞3或x＜2} | C． | {x|2≤x≤3} | D． | {x|2＜x＜3} |
13．已知坐标原点O（0，0）关于直线L对称的点是M（3，-3），则直线L的方程是（ ）
| A． | x-2y+1=0 | B． | 2x-y-1=0 | C． | x-y+3=0 | D． | x-y-3=0 |
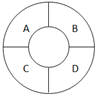如图，一环形花坛分成A、B、C、D四块，现有4种不同的花供选种，要求在每块里种一种花，且相邻的2块种不同的花，则不同的种法总数为84．
14．函数f（x）=x2-4x+5在区间[0，m]上的最大值为5，最小值为1，则实数m的取值范围是（ ）
| A． | [2，+∞） | B． | （2，4] | C． | [0，4] | D． | [2，4] |