题目内容
20．
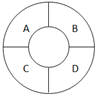如图，一环形花坛分成A、B、C、D四块，现有4种不同的花供选种，要求在每块里种一种花，且相邻的2块种不同的花，则不同的种法总数为84．
分析 分为三类：分别种两种花、三种花、四种花，可从4种不同的花先选再排，分这三类来列出结果，求和即可得到．
解答 解：分三类：种两种花有A42种种法；
种三种花有2A43种种法；
种四种花有A44种种法．
共有A42+2A43+A44=84．
故答案为：84．
点评 本题考查排列组合应用题的解法，注意运用分类和分步原理，考查运算能力，属于中档题．本题也可以这样解：按A-B-C-D顺序种花，可分A、C同色与不同色有4×3×（1×3+2×2）=84种．
练习册系列答案
相关题目
11．数列{an}满足a1=2，an+1=$\frac{{a}_{n}}{{a}_{n}+1}$，则a5的值为（ ）
| A． | $\frac{2}{5}$ | B． | $\frac{2}{7}$ | C． | $\frac{2}{9}$ | D． | $\frac{2}{11}$ |
5．已知动点M（x，y）的坐标满足$\sqrt{{{（x-2）}^2}+{y^2}}$=|x+2|，则动点M的轨迹是（ ）
| A． | 椭圆 | B． | 双曲线 | C． | 抛物线 | D． | 以上均不对 |
12．
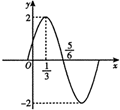已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象（部分）如图所示，则要得到y=f（x）的图象，只需要把y=Asinωx的图象（ ）
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象（部分）如图所示，则要得到y=f（x）的图象，只需要把y=Asinωx的图象（ ）| A． | 向左平移$\frac{π}{6}$个单位 | B． | 向右平移$\frac{π}{6}$个单位 | ||
| C． | 向左平移$\frac{1}{6}$个单位 | D． | 向右平移$\frac{1}{6}$个单位 |