题目内容

17．在等比数列{an}中，各项均为正值，且a6a10+a3a5=41，a4a8=5，则a4+a8=$\sqrt{51}$．

分析 由等比数列{an}中，各项均为正值，且a6a10+a3a5=41，可得${a}_{8}^{2}+{a}_{4}^{2}$=41，又a4a8=5，即可得出．

解答 解：由等比数列{an}中，各项均为正值，且a6a10+a3a5=41，
∴${a}_{8}^{2}+{a}_{4}^{2}$=41，又a4a8=5，
则a4+a8=$\sqrt{41+2×5}$=$\sqrt{51}$．
故答案为：$\sqrt{51}$．

点评 本题考查了等比数列的通项公式及其性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
7．若x，y满足约束条件$\left\{\begin{array}{l}{x-2y+1≤0}\\{2x-y+2≥0}\\{x+y-2≤0}\end{array}\right.$，z=3x+y+m的最大值为1，则m为（　　）
A．-1B．-3C．2D．3
8．直线3x-4y+2=0的单位法向量$\overrightarrow{n_0}$=$±（\frac{3}{5}，\frac{4}{5}）$．
5．已知动点M（x，y）的坐标满足$\sqrt{{{（x-2）}^2}+{y^2}}$=|x+2|，则动点M的轨迹是（　　）
A．椭圆B．双曲线C．抛物线D．以上均不对
12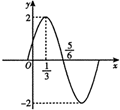．已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象（部分）如图所示，则要得到y=f（x）的图象，只需要把y=Asinωx的图象（　　）
A．向左平移$\frac{π}{6}$个单位B．向右平移$\frac{π}{6}$个单位
C．向左平移$\frac{1}{6}$个单位D．向右平移$\frac{1}{6}$个单位
2．过曲线C：y=ex上一点，然后再过P1（x1，y1）做曲线C的切线l1交x轴于Q2（x2，0），又过Q2做x轴P0（0，1）作曲线C的切线l0交x轴于点Q1（x1，0），又过Q1做x轴的垂线交曲线C于P1（x1，y1）的垂线交曲线C于点P2（x2，y2），…，以此类推，过点Pn的切线ln与x轴相交于点Qn+1（xn+1，0），再过点Qn+1做x轴的垂线交曲线C于点Pn+1（xn+1，yn+1）（n=1，2，3，…）．
（1）求x1、x2及数列{xn}的通项公式；
（2）设曲线C与切线ln及垂线Pn+1Qn+1所围成的图形面积为Sn，求Sn的表达式；
（3）在满足（2）的条件下，若数列Sn的前n项和为Tn，求证：$\frac{{{T_{n+1}}}}{T_n}$＜$\frac{{{x_{n+1}}}}{x_n}$（n∈N*）
9．掷一枚骰子，观察掷出的点数，则事件“掷出奇数点或3的倍数”的概率为$\frac{2}{3}$．
6．计算下列各式的值：
（1）8${\;}^{\frac{2}{3}$+（0.01）${\;}^{-\frac{1}{2}}}$+（$\frac{1}{27}$）${\;}^{-\frac{1}{3}}$；
（2）21g5+$\frac{2}{3}$lg8+lg5•lg20+（lg2）2．
10．若a，b是异面直线，b，c是异面直线，则（　　）
A．a∥cB．a，c是异面直线
C．a，c相交D．a，c的位置关系不确定

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网