��Ŀ����
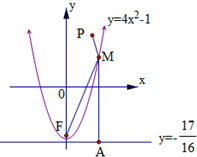
��֪�����ߵķ���Ϊy=ax2-1��ֱ��l�ķ���Ϊy=
����A��3��-1������ֱ��l�ĶԳƵ����������ϣ�
��1���������ߵķ��̣�
��2����֪P��
��1������F��0��-
���������ߵĽ��㣬M���������ϵĶ��㣬��|MP|+|MF|����Сֵ����ʱ��M�����ꣻ
��3�����B��C���������ϵĶ��㣬��D����������x�������ύ�㣬��BCD����DΪֱ�Ƕ����ֱ�������Σ���̽��ֱ��BC�Ƿ����㣿�������������������ꣻ������������˵�����ɣ�
| x |
| 2 |
��1���������ߵķ��̣�
��2����֪P��
| 1 |
| 2 |
| 15 |
| 16 |
��3�����B��C���������ϵĶ��㣬��D����������x�������ύ�㣬��BCD����DΪֱ�Ƕ����ֱ�������Σ���̽��ֱ��BC�Ƿ����㣿�������������������ꣻ������������˵�����ɣ�
���㣺ֱ����Բ���ߵ��ۺ�����
ר�⣺Բ�����е���ֵ�뷶Χ����
��������1������֪���������A��3��-1������ֱ��l�ĶԳƵ�Ϊ����A�䣨1��3������A�䣨1��3������y=ax2-1�����a=4���ɴ�����������ߵķ��̣�
��2����F��0��-
���������ߵĽ��㣬�����ߵĶ���Ϊ��0��-1������������ߵ���Ϊx=-
���ɴ������|MP|+|MF|����Сֵ����ʱ��M�����꣮
��3��BC���ڵ�ֱ�߾������㣨-
��
������y=4x2-1=0����D���������
��0��������ֱ�ߴ�ֱ�����ʺ�ֱ��б�ʵĹ�ϵ�����ֱ��BC�ķ���Ϊ��y=2��x1+x2����2x+1��+
���ɴ���֤��ֱ��BC�������㣨-
��
����
��2����F��0��-
| 15 |
| 16 |
| 17 |
| 16 |
��3��BC���ڵ�ֱ�߾������㣨-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
���
�⣺��1�����A��3��-1������ֱ��l�ĶԳƵ�Ϊ����ΪA�䣨x��y����
 ��
��
�����
����3�֣�
�ѵ�A�䣨1��3������y=ax2-1�����a=4��
�������ߵķ���Ϊy=4x2-1����4�֣�
��2����F��0��-
���������ߵĽ��㣬�����ߵĶ���Ϊ��0��-1����
�������ߵ���Ϊx=-
����5�֣�
����M���ߵĴ��ߣ�����ΪA���������ߵĶ���֪|MF|=|MA|��
��|MP|+|MF|=|MP|+|MA|��|PA|��
���ҽ���P��M��A���㹲��ʱ��=����������7�֣�
������MΪ����P�������������ߵĴ����������ߵĽ���ʱ��
|MP|+|MF|ȡ��Сֵ��
�ࣨ|MP|+|MF|��min=1-��-
��=
��
��ʱ��M������Ϊ��
��0������9�֣�
��3��BC���ڵ�ֱ�߾������㣬�ö�������Ϊ��-
��
����
��y=4x2-1=0����D���������
��0����
��B��x1��y1����C��x2��y2����x1��x2��
��kBC=
=
=4��x1+x2������10�֣�
kBD=4(x1+
)��kCD=4(x2+
)����11�֣�
��BD��CD����kBD•kCD=16(x1+
)(x2+
)=-1��
��x1x2=-
-
(x1+x2)��
ֱ��BC�ķ���Ϊy-y1=4��x1+x2����x-x1����
��y=4��x1+x2��x-4x1 x2-1=2��x1+x2����2x+1��+
����13�֣�
��ֱ��BC�������㣨-
��
������14�֣�
 ��
��
|
|
�ѵ�A�䣨1��3������y=ax2-1�����a=4��
�������ߵķ���Ϊy=4x2-1����4�֣�
��2����F��0��-
| 15 |
| 16 |
�������ߵ���Ϊx=-
| 17 |
| 16 |
����M���ߵĴ��ߣ�����ΪA���������ߵĶ���֪|MF|=|MA|��
��|MP|+|MF|=|MP|+|MA|��|PA|��
���ҽ���P��M��A���㹲��ʱ��=����������7�֣�
������MΪ����P�������������ߵĴ����������ߵĽ���ʱ��
|MP|+|MF|ȡ��Сֵ��
�ࣨ|MP|+|MF|��min=1-��-
| 17 |
| 16 |
| 33 |
| 16 |
��ʱ��M������Ϊ��
| 1 |
| 2 |
��3��BC���ڵ�ֱ�߾������㣬�ö�������Ϊ��-
| 1 |
| 2 |
| 1 |
| 4 |
��y=4x2-1=0����D���������
| 1 |
| 2 |
��B��x1��y1����C��x2��y2����x1��x2��
��kBC=
| y 1-y2 |
| x1-x2 |
| 4(x12-x22) |
| x1-x2 |
kBD=4(x1+
| 1 |
| 2 |
| 1 |
| 2 |
��BD��CD����kBD•kCD=16(x1+
| 1 |
| 2 |
| 1 |
| 2 |
��x1x2=-
| 5 |
| 16 |
| 1 |
| 2 |
ֱ��BC�ķ���Ϊy-y1=4��x1+x2����x-x1����
��y=4��x1+x2��x-4x1 x2-1=2��x1+x2����2x+1��+
| 1 |
| 4 |
��ֱ��BC�������㣨-
| 1 |
| 2 |
| 1 |
| 4 |
���������⿼�������߷��̵������������߶κ���Сֵ��������ֱ�߹�������ж���֤��������ʱҪ�������⣬ע��ȼ�ת��˼��ͺ����뷽��˼��ĺ������ã�

��ϰ��ϵ�д�
�����Ŀ
