题目内容
13.函数f(x)=asin(2x+$\frac{π}{6}$)+bcos2x(a、b不全为零)的最小正周期为( )| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
分析 根据正弦、余弦型函数的周期T=$\frac{2π}{|ω|}$,直接求出f(x)的最小正周期即可.
解答 解:函数f(x)=asin(2x+$\frac{π}{6}$)+bcos2x
=$\frac{\sqrt{3}}{2}$asin2x+$\frac{1}{2}$acos2x+bcos2x
=$\frac{\sqrt{3}}{2}$asin2x+($\frac{1}{2}$a+b)cos2x
=$\sqrt{{\frac{3}{4}a}^{2}{+(\frac{1}{2}a+b)}^{2}}$sin(2x+θ),其中tanθ=$\frac{\frac{1}{2}a+b}{\frac{\sqrt{3}}{2}a}$;
∴f(x)的最小正周期为T=$\frac{2π}{2}$=π.
故选:B.
点评 本题考查了正弦、余弦型函数的最小正周期问题,是基础题.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
18.已知角α的终边与单位圆x2+y2=1的交点为$P\;(x\;,\frac{{\sqrt{3}}}{2})$,则cos2α=( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | 1 |
5.给出下列两个命题:命题p:若在边长为1的正方形ABCD内任取一点M,则|MA|≤1的概率为$\frac{π}{4}$.命题q:若函数f(x)=x+$\frac{4}{x}$,(x∈[1,2)),则f(x)的最小值为4.则下列命题为真命题的是( )
| A. | p∧q | B. | ¬p | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
10.已知函数f(x)=$\left\{{\begin{array}{l}{lnx,x>0}\\{\frac{m}{x},x<0}\end{array}}$,若f(x)-f(-x)=0有四个不同的根,则m的取值范围是( )
| A. | (0,2e) | B. | (0,e) | C. | (0,1) | D. | (0,$\frac{1}{e}$) |
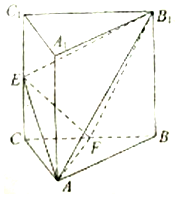 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,E,F分别是CC1,BC的中点,且AB=AA1.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,E,F分别是CC1,BC的中点,且AB=AA1.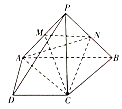 如图所示,四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥CD,AD⊥CD,PC⊥
如图所示,四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥CD,AD⊥CD,PC⊥