题目内容
10.已知函数f(x)=$\left\{{\begin{array}{l}{lnx,x>0}\\{\frac{m}{x},x<0}\end{array}}$,若f(x)-f(-x)=0有四个不同的根,则m的取值范围是( )| A. | (0,2e) | B. | (0,e) | C. | (0,1) | D. | (0,$\frac{1}{e}$) |
分析 由函数图象的对称性可得f(x)-f(-x)在(0,+∞)上有两解,分离参数得-m=xlnx,求出右侧函数的单调性和极值即可得出m的范围.
解答 解:∵f(x)-f(-x)=0有四个不同的根,
且y=f(x)与y=f(-x)的图象关于y轴对称,
∴f(x)=f(-x)在(0,+∞)上有2解,
即lnx=-$\frac{m}{x}$有2解,∴-m=xlnx有2解,
令g(x)=xlnx,则g′(x)=lnx+1,
∴当0<x$<\frac{1}{e}$时,g′(x)<0,当x>$\frac{1}{e}$时,g′(x)>0,
∴g(x)在(0,$\frac{1}{e}$)上单调递减,在($\frac{1}{e}$,+∞)上单调递增,
当x=$\frac{1}{e}$时,f(x)取得极小值f($\frac{1}{e}$)=-$\frac{1}{e}$.
作出g(x)的大致函数图象如图所示: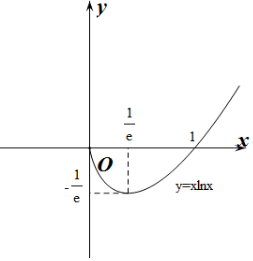
∵-m=xlnx有两解,
∴-$\frac{1}{e}$<-m<0,即0<m<$\frac{1}{e}$.
故选D.
点评 本题考查方程的根与函数的图象的关系,函数单调性判断与极值计算,属于中档题.

练习册系列答案
相关题目
13.函数f(x)=asin(2x+$\frac{π}{6}$)+bcos2x(a、b不全为零)的最小正周期为( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
1.已知Rt△ABC,AB=3,BC=4,CA=5,P为△ABC外接圆上的一动点,且$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{AC},则x+y$的最大值是( )
| A. | $\frac{5}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{{\sqrt{17}}}{6}$ | D. | $\frac{5}{3}$ |
18.对两个变量x、y进行线性回归分析,计算得到相关系数r=-0.9962,则下列说法中正确的是( )
| A. | x与y正相关 | |
| B. | x与y具有较强的线性相关关系 | |
| C. | x与y几乎不具有线性相关关系 | |
| D. | x与y的线性相关关系还需进一步确定 |
5.与抛物线y=2x2关于直线y=x对称的抛物线的准线方程为( )
| A. | $x=\frac{1}{8}$ | B. | $x=\frac{1}{2}$ | C. | $x=-\frac{1}{8}$ | D. | $x=-\frac{1}{2}$ |
15.设正实数x,y,则|x-y|+$\frac{1}{x}$+y2的最小值为( )
| A. | $\frac{7}{4}$ | B. | $\frac{3\root{3}{2}}{2}$ | C. | 2 | D. | $\root{3}{2}$ |