题目内容
5．在△ABC中，AB=2BC，∠B=120°．若以A，B为焦点的椭圆经过点C，则该椭圆的离心率e为$\frac{{-1+\sqrt{7}}}{3}$．分析 利用余弦定理求得丨AC丨，由椭圆的定义可知：丨AC丨+丨BC丨=2a，2c=2，由e=$\frac{c}{a}$，即可求得椭圆的离心率．
解答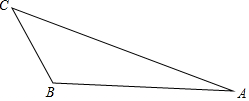 
解：设丨AB丨=2丨BC丨=2，则丨AC丨2=丨AB丨2+丨BC丨2-2丨AB丨•丨BC丨•cosB=4+1-2×4×1×（-$\frac{1}{2}$）=7，
∴丨AC丨=$\sqrt{7}$，
∵以A、B为焦点的椭圆经过点C，
∴2a=$\sqrt{7}$+1，2c=2
∴e=$\frac{c}{a}$=$\frac{2}{\sqrt{7}+1}$=$\frac{{-1+\sqrt{7}}}{3}$，
故答案为：$\frac{{-1+\sqrt{7}}}{3}$．
点评 本题考查椭圆的标准方程及简单几何性质，考查余弦定理，属于基础题．
练习册系列答案
相关题目
15．过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点F作圆x2+y2=a2的切线，切点为E，延长FE交双曲线于点P，O为坐标原点，若$\overrightarrow{OE}$=$\frac{1}{2}$（$\overrightarrow{OF}$+$\overrightarrow{OP}$），则双曲线的离心率为（ ）
| A． | $\frac{1+\sqrt{5}}{2}$ | B． | $\frac{\sqrt{5}}{2}$ | C． | $\sqrt{5}$ | D． | $\frac{1+\sqrt{3}}{2}$ |
16．设函数f（x）和g（x）分别是R上的偶函数和奇函数，则下列结论恒成立的是（ ）
| A． | f（x）•|g（x）|是奇函数 | B． | f（x）+|g（x）|是偶函数 | C． | |f（x）|-g（x）是奇函数 | D． | |f（x）|•g（x）是偶函数 |
10．设函数f（x）的定义域为R，且|f（x）|是偶函数，则下列结论中正确的是（ ）
| A． | f（x）是偶函数 | B． | f（x）是奇函数 | ||
| C． | |f（x-1）|的图象关于直线x=1对称 | D． | |f（x）+1|的图象关于点（0，1）对称 |
15．设f（x）=$\left\{\begin{array}{l}{1-\sqrt{x}，x≥0}\\{{2}^{x}，x＜0}\end{array}\right.$，则f（f（-log23））=（ ）
| A． | $\frac{3-\sqrt{3}}{3}$ | B． | $\frac{3}{2}$ | C． | 1-$\sqrt{3}$ | D． | $\sqrt{3}$-1 |