题目内容
15.设f(x)=$\left\{\begin{array}{l}{1-\sqrt{x},x≥0}\\{{2}^{x},x<0}\end{array}\right.$,则f(f(-log23))=( )| A. | $\frac{3-\sqrt{3}}{3}$ | B. | $\frac{3}{2}$ | C. | 1-$\sqrt{3}$ | D. | $\sqrt{3}$-1 |
分析 先求出f(-log23)=${2}^{-lo{g}_{2}3}$=${2}^{lo{g}_{2}\frac{1}{3}}$=$\frac{1}{3}$,从而f(f(-log23))=f($\frac{1}{3}$),由此能求出结果.
解答 解:∵f(x)=$\left\{\begin{array}{l}{1-\sqrt{x},x≥0}\\{{2}^{x},x<0}\end{array}\right.$,
∴f(-log23)=${2}^{-lo{g}_{2}3}$=${2}^{lo{g}_{2}\frac{1}{3}}$=$\frac{1}{3}$,
f(f(-log23))=f($\frac{1}{3}$)=1-$\sqrt{\frac{1}{3}}$=$\frac{3-\sqrt{3}}{3}$.
故选:A.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
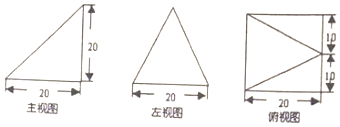
7.《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“盖”的术:置如其周,令相承也.又以高乘之,三十六成一.该术相当于给出了有圆锥的底面周长L与高,计算其体积V的近似公式V≈$\frac{1}{48}$L2h,它实际上是将圆锥体积公式中的圆周率π近似取为4,那么近似公式V≈$\frac{1}{75}$L2h相当于将圆锥体积公式中π的近似取为( )
| A. | $\frac{25}{6}$ | B. | $\frac{25}{8}$ | C. | $\frac{25}{3}$ | D. | $\frac{25}{4}$ |
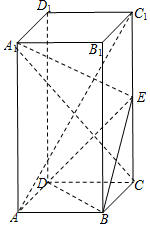 在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为棱CC1上的动点.
在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为棱CC1上的动点.