题目内容
16.设函数f(x)和g(x)分别是R上的偶函数和奇函数,则下列结论恒成立的是( )| A. | f(x)•|g(x)|是奇函数 | B. | f(x)+|g(x)|是偶函数 | C. | |f(x)|-g(x)是奇函数 | D. | |f(x)|•g(x)是偶函数 |
分析 由设函数f(x)和g(x)分别是R上的偶函数和奇函数,我们易得到|f(x)|、|g(x)|也为偶函数,进而根据奇+奇=奇,偶+偶=偶,即可得到答案.
解答 解:∵函数f(x)和g(x)分别是R上的偶函数和奇函数,
∴|g(x)|也为偶函数,
∴f(x)+|g(x)|是偶函数,
故选B.
点评 本题考查的知识点是函数奇偶性的判断,其中根据已知确定|f(x)|、|g(x)|也为偶函数,是解答本题的关键.

练习册系列答案
相关题目
6.直线x+y+1=0关于点(1,2)对称的直线方程为( )
| A. | x+y-7=0 | B. | x-y+7=0 | C. | x+y+6=0 | D. | x-y-6=0 |
7.已知可导函数f(x)(x∈R)的导数f′(x)满足f′(x)-f(x)<0,则( )
| A. | ef(2015)>f(2016) | B. | ef(2015)<f(2016) | ||
| C. | ef(2015)=f(2016) | D. | ef(2015)与f(2016)的大小不确定 |
4.函数f(x)=x2-f'(-1)x+1在x=1处的切线方程为( )
| A. | y=-x+4 | B. | y=3x | C. | y=3x-3 | D. | y=3x-9 |
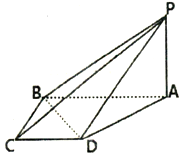 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,PA=1.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,PA=1.