题目内容
13.若tanα=2,则$\frac{sinα+2cosα}{2sinα-cosα}$+cosαsinα等于$\frac{26}{15}$.分析 利用弦化切与平方和公式,化简求值即可.
解答 解:tanα=2,
则$\frac{sinα+2cosα}{2sinα-cosα}$+cosαsinα
=$\frac{sinα+2cosα}{2sinα-cosα}$+$\frac{cosαsinα}{{sin}^{2}α{+cos}^{2}α}$
=$\frac{tanα+2}{2tanα-1}$+$\frac{tanα}{{tan}^{2}α+1}$
=$\frac{2+2}{2×2-1}$+$\frac{2}{{2}^{2}+1}$
=$\frac{4}{3}$+$\frac{2}{5}$
=$\frac{26}{15}$.
故答案为:$\frac{26}{15}$.
点评 本题考查了三角函数化简与求值问题,是基础题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
3.直线l与抛物线y2=6x交于A,B两点,圆(x-6)2+y2=r2与直线l相切于点M,且M为线段AB的中点.若这样的直线l恰有4条,则r的取值范围是( )
| A. | ($\sqrt{3}$,2$\sqrt{3}$) | B. | ($\sqrt{3}$,3$\sqrt{3}$) | C. | (3,$2\sqrt{3}$) | D. | (3,3$\sqrt{3}$) |
4.函数f(x)=x2-f'(-1)x+1在x=1处的切线方程为( )
| A. | y=-x+4 | B. | y=3x | C. | y=3x-3 | D. | y=3x-9 |
2.下列选项中方程表示图中曲线的是( )
| A. |  x2+y2=1 | B. |  x2-y2=0 | C. |  y=|x| | D. |  lgx+lgy=0 |
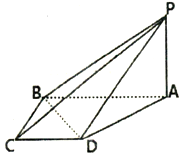 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,PA=1.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,PA=1.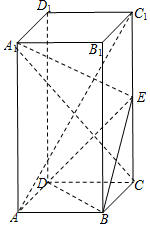 在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为棱CC1上的动点.
在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为棱CC1上的动点.