题目内容
15.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点F作圆x2+y2=a2的切线,切点为E,延长FE交双曲线于点P,O为坐标原点,若$\overrightarrow{OE}$=$\frac{1}{2}$($\overrightarrow{OF}$+$\overrightarrow{OP}$),则双曲线的离心率为( )| A. | $\frac{1+\sqrt{5}}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{1+\sqrt{3}}{2}$ |
分析 由题设知|EF|=b,|PF|=2b,|PF'|=2a,再由|PF|-|PF'|=2a,知b=2a,由此能求出双曲线的离心率.
解答 解:∵|OF|=c,|OE|=a,OE⊥EF,∴|EF|=b,
∵$\overrightarrow{OE}$=$\frac{1}{2}$($\overrightarrow{OF}$+$\overrightarrow{OP}$),则),∴|PF|=2b,|PF'|=2a,
∵|PF|-|PF'|=2a,∴b=2a,
e=$\sqrt{1+(\frac{b}{a})^{2}}=\sqrt{5}$,
故选:C
点评 本题主要考查双曲线的标准方程,以及双曲线的简单性质的应用,考查双曲线的定义,考查运算求解能力,考查数形结合思想、化归与转化思想,属于中档题.

练习册系列答案
相关题目
5.已知a>0,-1<b<0,那么下列不等式成立的是( )
| A. | a<ab<ab2 | B. | ab<a<ab2 | C. | ab<ab2<a | D. | ab2<a<ab |
6.直线x+y+1=0关于点(1,2)对称的直线方程为( )
| A. | x+y-7=0 | B. | x-y+7=0 | C. | x+y+6=0 | D. | x-y-6=0 |
3.直线l与抛物线y2=6x交于A,B两点,圆(x-6)2+y2=r2与直线l相切于点M,且M为线段AB的中点.若这样的直线l恰有4条,则r的取值范围是( )
| A. | ($\sqrt{3}$,2$\sqrt{3}$) | B. | ($\sqrt{3}$,3$\sqrt{3}$) | C. | (3,$2\sqrt{3}$) | D. | (3,3$\sqrt{3}$) |
10.若直线ax-by+1=0(a>0,b>0)分圆C:x2+y2+2x-4y+1=0的周长,则ab的取值范围是( )
| A. | (-∞,$\frac{1}{8}$] | B. | (0,$\frac{1}{8}$] | C. | (0,$\frac{1}{4}$] | D. | [$\frac{1}{4}$,+∞) |
7.已知可导函数f(x)(x∈R)的导数f′(x)满足f′(x)-f(x)<0,则( )
| A. | ef(2015)>f(2016) | B. | ef(2015)<f(2016) | ||
| C. | ef(2015)=f(2016) | D. | ef(2015)与f(2016)的大小不确定 |
4.函数f(x)=x2-f'(-1)x+1在x=1处的切线方程为( )
| A. | y=-x+4 | B. | y=3x | C. | y=3x-3 | D. | y=3x-9 |
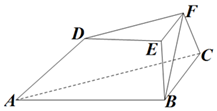 如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.
如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.