题目内容
将一枚质地均匀的骰子抛掷一次出现“正面向上的点数为2或3”的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：古典概型及其概率计算公式
专题：概率与统计
分析：根据古典槪型的概率公式即可得到结论．
解答：
解：将一枚质地均匀的骰子抛掷一次共有6个结果，
则出现“正面向上的点数为2或3”，包含2个结果，
则出现“正面向上的点数为2或3”的概率P=
=
，
故选：C
则出现“正面向上的点数为2或3”，包含2个结果，
则出现“正面向上的点数为2或3”的概率P=
| 2 |
| 6 |
| 1 |
| 3 |
故选：C
点评：本题主要考查概率的计算，利用古典概率的公式是解决本题的关键，比较基础．
练习册系列答案
相关题目
已知角θ的顶点与原点重合，始边与x轴的正半轴重合，终边在直线y=
x上，则sin2θ=（ ）
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数y=sinax+b（a＞0）某一个周期的图象如图所示，则函数f（x）=ax2+bx+1零点的个数有（ ）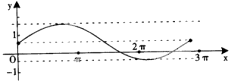
| A、0 | B、1 | C、2 | D、无法确定 |
已知集合U={0，1，2，3，4}，A={x|x2-2x=0}，则∁UA=（ ）
| A、{1，2，3} |
| B、{0，1，3，4} |
| C、{1，3，4} |
| D、{0，3，4} |
z=
，则|z|=（ ）
| 5+12i |
| 3+4i |
A、
| ||
B、
| ||
C、
| ||
D、
|
若实数x，y满足
，则z=x+2y的最小值是（ ）
|
| A、0 | ||
B、
| ||
| C、5 | ||
| D、1 |
设复数ω=-
+
i（i为虚数单位），则（ω+1）2=（ ）
| 1 |
| 2 |
| ||
| 2 |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
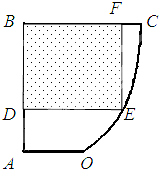某同学的数学研究性学习课题是：在校内一块不规则土地OABC（测绘图如图所示）规划一个矩形运动场地．经过测量发现AB⊥BC，OA∥BC，曲线段OC可近似看作是以点O为顶点且开口向上的抛物线的一段，OA=20m，AB=BC=40m．