题目内容
4.若复数z满足iz=l+3i,其中i为虚数单位,则$\overline z$=( )| A. | -3+i | B. | -3-i | C. | 3+i | D. | 3-i |
分析 利用复数的运算法则、共轭复数的定义即可得出.
解答 解:iz=l+3i,∴-i•iz=-i(l+3i),∴z=-i+3.
则$\overline z$=3+i.
故选:C.
点评 本题考查了复数的运算法则、共轭复数的定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.设变量x,y满足约束条件$\left\{\begin{array}{l}x-2y+1≤0\\ x+y-5≤0\\ 4x-2y+1≥0\end{array}\right.$,若目标函数z=mx-y取得最大值的最优解有无数个,则m=( )
| A. | $\frac{1}{2}$ | B. | -1 | C. | 2 | D. | $-1或\frac{1}{2}$ |
13.已知命题p:?x∈R,x2-mx+1=0,q:?x∈R,ex-m>0,若¬p∧q为真,则实数m的取值范围是( )
| A. | [-2,2] | B. | (-2,0] | C. | (-2,0) | D. | [0,2] |
14.已知函数f(x)=2017x+log2017($\sqrt{{x^2}+1}$+x)-2017-x+2,则关于x的不等式f(3x+1)+f(x)>4的解集为( )
| A. | $(-∞,-\frac{1}{4})$ | B. | $(-\frac{1}{4},+∞)$ | C. | (0,+∞) | D. | (-∞,0) |
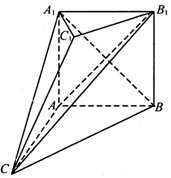 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,A1C=BC,B1C1∥BC,且${B_1}{C_1}=\frac{1}{2}BC$.
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,A1C=BC,B1C1∥BC,且${B_1}{C_1}=\frac{1}{2}BC$.