题目内容
12.己知等比数列{an}的前n项和为Sn,a1=1,S6=9S3(I )求{an}的通项公式
(II)设bn=1+log2an,求数列{anbn}的前n项和.
分析 (I)利用等比数列的通项公式与求和公式即可得出.
(II)利用错位相减法、等比数列的求和公式即可得出.
解答 解:(Ⅰ)设等比数列{an}的公比为q,
∵a1=1,S6=9S3,知q≠1,故有$\frac{1-{q}^{6}}{1-q}$=$\frac{9(1-{q}^{3})}{1-q}$,
即(1-q3)(1+q3)=9(1-q3),
即有1+q3=9,即q3=8,解得q=2,…(4分)
则an=a1qn-1=2n-1…(6分)
$(Ⅱ){b}_{n}=1+{log}_{2}{a}_{n}=1+{log}_{2}{2}^{n-1}=1+n-1=n$,
∴${a}_{n}{b}_{n}=n•{2}^{n-1}…(7分)$,
∴${T}_{n}=1+2•2+3•{2}^{2}+…+n•{2}^{n-1}①$
$2{T}_{n}=1•2+2•{2}^{2}+…(n-1){2}^{n-1}+n•{2}^{n}②$
②-①得${T}_{n}=n•{2}^{n}-(1+2+{2}^{2}+…+{2}^{n-1})=n•{2}^{n}-({2}^{n}-1)=(n-1){2}^{n}+1…(12分)$
点评 本题考查了等比数列的通项公式求和公式、错位相减法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
20.已知命题p:函数f(x)=|cos2x-sinxcosx-$\frac{1}{2}$|的最小正周期为π;命题q:函数f(x)=ln$\frac{3+x}{3-x}$的图象关于原点中心对称,则下列命题是真命题的是( )
| A. | p∧q | B. | p∨q | C. | (¬p)∧(¬q) | D. | p∨(¬q) |
7.己知复数$\frac{2+i}{a-i}$(其中a∈R,i是虚数单位)是纯虚数,则a的值为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
4.若复数z满足iz=l+3i,其中i为虚数单位,则$\overline z$=( )
| A. | -3+i | B. | -3-i | C. | 3+i | D. | 3-i |
1.已知集合$A=\{x|y=\sqrt{2x-{x^2}}\}$,B={x|-1<x<1},则A∪B=( )
| A. | [0,1) | B. | (-1,2) | C. | (-1,2] | D. | (-∞,0]∪(1,+∞) |
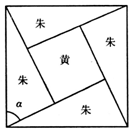 三国时代吴国数学家赵爽所著《周髀算经》中用赵爽弦图给出了勾股定理的绝妙证明,如图是赵爽弦图,图中包含四个全等的勾股形及一个小正方形,分别涂成朱色和黄色,若朱色的勾股形中较大的锐角α为$\frac{π}{3}$,现向该赵爽弦图中随机地投掷一枚飞镖,则飞镖落在黄色的小正方形内的概率为1-$\frac{\sqrt{3}}{2}$.
三国时代吴国数学家赵爽所著《周髀算经》中用赵爽弦图给出了勾股定理的绝妙证明,如图是赵爽弦图,图中包含四个全等的勾股形及一个小正方形,分别涂成朱色和黄色,若朱色的勾股形中较大的锐角α为$\frac{π}{3}$,现向该赵爽弦图中随机地投掷一枚飞镖,则飞镖落在黄色的小正方形内的概率为1-$\frac{\sqrt{3}}{2}$.