题目内容
14.已知{an}为等比数列,Sn是它的前n项和.若${a_3}{a_5}=\frac{1}{4}{a_1}$,且a4与a7的等差中项为$\frac{9}{8}$,则S5为31.分析 利用等比数列的通项公式与求和公式即可得出.
解答 解:设等比数列{an}的公比为q,∵a4与a7的等差中项为$\frac{9}{8}$,
∴a4+a7=2×$\frac{9}{8}$,
∴${a}_{1}({q}^{3}+{q}^{6})$=$\frac{9}{4}$,
∵${a_3}{a_5}=\frac{1}{4}{a_1}$,∴${a}_{1}^{2}{q}^{6}$=$\frac{1}{4}{a}_{1}$,
联立解得:q=$\frac{1}{2}$,a1=16.
∴S5=$\frac{16(1-\frac{1}{{2}^{5}})}{1-\frac{1}{2}}$=31.
故答案为:31.
点评 本题考查了等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
9.甲、乙、丙、丁四人参加国际奥林匹克数学竞赛选拔赛,四人的平均成绩和方差如表:
从这四人中选择一人参加国际奥林匹克数学竞赛,最佳人选是( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均成绩$\overline x$ | 89 | 89 | 86 | 85 |
| 方差S2 | 2.1 | 3.5 | 2.1 | 5.6 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
6.非空集A={x|2a+1≤x≤3a-5},B=$\{x|y=\sqrt{(3-x)(x-22)}\}$,则A⊆A∩B的一个充分不必要条件是( )
| A. | 1≤a≤9 | B. | 6<a<9 | C. | 6≤a≤9 | D. | a≤9 |
3.若cosα=$\frac{1}{2}$,α∈(0,π),则cos($\frac{π}{2}$-α)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
4.已知a=2${\;}^{\frac{4}{3}}$,b=3${\;}^{\frac{2}{3}}$,c=2.5${\;}^{\frac{1}{3}}$,则( )
| A. | a<b<c | B. | c<b<a | C. | b<c<a | D. | c<a<b |
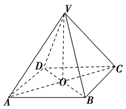 如图所示,四棱锥V-ABCD的底面为边长等于2cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4cm,求这个正四棱锥的体积.
如图所示,四棱锥V-ABCD的底面为边长等于2cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4cm,求这个正四棱锥的体积.