题目内容
4．已知a=2${\;}^{\frac{4}{3}}$，b=3${\;}^{\frac{2}{3}}$，c=2.5${\;}^{\frac{1}{3}}$，则（ ）| A． | a＜b＜c | B． | c＜b＜a | C． | b＜c＜a | D． | c＜a＜b |
分析 利用指数函数、对数函数的单调性求解．
解答 解：∵a=2${\;}^{\frac{4}{3}}$=16${\;}^{\frac{1}{3}}$，
b=3${\;}^{\frac{2}{3}}$=9${\;}^{\frac{1}{3}}$，c=2.5${\;}^{\frac{1}{3}}$，
y=x${\;}^{\frac{1}{3}}$在（0，+∞）是增函数，
∴c＜b＜a．
故选：B．
点评 本题考查三个数的大小的比较，是基础题，解题时要认真审题，注意指数函数、对数函数的单调性的合理运用．
练习册系列答案
相关题目
15．下列说法中正确的是（ ）
| A． | 若p∨q为真命题，则p，q均为真命题 | |
| B． | “a≥5”是“?x∈[1，2]，x2-a≤0恒成立“的充要条件 | |
| C． | 在△ABC中，“a＞b”是“sinA＞sinB”的必要不充分条件 | |
| D． | 命题“?x0∈R，2x0≤0”的否定是“?x∈R，2x＞0” |
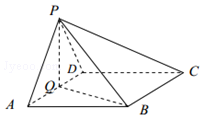如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点．