题目内容
19．函数y=log5x的定义域（ ）| A． | （-∞，0） | B． | （-∞，0] | C． | （0，+∞） | D． | [0，+∞） |
分析 根据题意，由对数函数的定义域可得x＞0，即可得答案．
解答 解：根据题意，函数y=log5x的是对数函数，
则有x＞0，即其定义域为（0，+∞）；
故选：C．
点评 本题考查对数函数的定义域，关键是掌握对数函数的性质．
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
10．过抛物线y2=4x的焦点F作直线l交抛物线于A，B两点，若$\frac{1}{|AF|}-\frac{1}{|BF|}$=$\frac{1}{2}$，则直线l的倾斜角θ（0＜θ＜$\frac{π}{2}$）等于（ ）
| A． | $\frac{π}{2}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{6}$ |
7．若正三棱锥的侧面都是直角三角形，则它的侧棱与底面所成角的余弦值为（ ）
| A． | $\frac{\sqrt{6}}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{\sqrt{2}}{3}$ | D． | $\frac{1}{3}$ |
14．设集合A={1，2，3}，B={2，4，6，8}，则A∩B=（ ）
| A． | {2} | B． | {2，3} | C． | {1，2，3，4，6，8} | D． | {1，3} |
4．已知a=$\frac{1}{6}$ln8，b=$\frac{1}{2}$ln5，c=ln$\sqrt{6}$-ln$\sqrt{2}$，则（ ）
| A． | a＜b＜c | B． | a＜c＜b | C． | c＜a＜b | D． | c＜b＜a |
11．若复数z满足：z+2i=$\frac{3-{i}^{3}}{1+i}$（i为虚数单位），则|z|等于（ ）
| A． | $\sqrt{13}$ | B． | 3 | C． | 5 | D． | $\sqrt{5}$ |
8．如图为某几何体的三视图，则该几何体的内切球的直径为（ ）
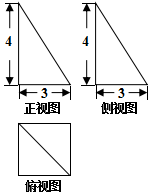
| A． | 2 | B． | 1 | C． | $\frac{1}{2}$ | D． | 4 |