题目内容
4．已知a=$\frac{1}{6}$ln8，b=$\frac{1}{2}$ln5，c=ln$\sqrt{6}$-ln$\sqrt{2}$，则（ ）| A． | a＜b＜c | B． | a＜c＜b | C． | c＜a＜b | D． | c＜b＜a |
分析 直接利用对数的性质判断大小即可．
解答 解：a=$\frac{1}{6}$ln8=$\frac{1}{2}ln2$，b=$\frac{1}{2}$ln5，c=ln$\sqrt{6}$-ln$\sqrt{2}$=$\frac{1}{2}ln3$，
∵ln2＜ln3＜ln5，
∴a＜c＜b．
故选：B．
点评 本题考查对数值大小的比较，考查函数的单调性的应用，是基础题．
练习册系列答案
相关题目
19．函数y=log5x的定义域（ ）
| A． | （-∞，0） | B． | （-∞，0] | C． | （0，+∞） | D． | [0，+∞） |
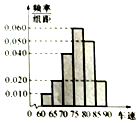交警随机抽取了途经某服务站的40辆小型轿车在经过某区间路段的车速（单位：km/h），现将其分成六组为[60，65），[65，70），[70，75），[75，80），[80，85），[85，90]后得到如图所示的频率分布直方图．
13．“α=$\frac{π}{6}$”是$tan（{π-a}）=-\frac{{\sqrt{3}}}{3}$的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分又不必要条件 |