题目内容
8.如图为某几何体的三视图,则该几何体的内切球的直径为( )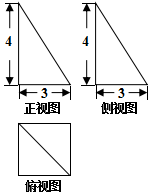
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | 4 |
分析 由已知中的三视图可得:该几何体是一个四棱锥,根据棱锥内切球半径公式,可得答案.
解答 解:由已知中的三视图可得:该几何体是一个四棱锥,
棱锥的体积V=$\frac{1}{3}$×3×3×4=12,
棱锥的表面积S=3×3+2×$\frac{1}{2}$×3×4+2×$\frac{1}{2}$×3×5=36,
故棱锥的内切球半径r=$\frac{3V}{S}$=1,
故该几何体的内切球的直径为2,
故选:A.
点评 本题考查的知识点是球的体积和表面积,锥的内切球半径,简单几何体的三视图,难度中档.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
18.已知复数$z=\frac{5}{2i-1}$(i为虚数单位),则z的共轭复数对应的点位于复平面的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.函数y=log5x的定义域( )
| A. | (-∞,0) | B. | (-∞,0] | C. | (0,+∞) | D. | [0,+∞) |
3.如图所示,在正方体ABCD-A1B1C1D1中,下列结论正确的是( )


| A. | 直线A1B与直线AC所成的角是45° | |
| B. | 直线A1B与平面ABCD所成的角是30° | |
| C. | 二面角A1-BC-A的大小是60° | |
| D. | 直线A1B与平面A1B1CD所成的角是30° |
13.“α=$\frac{π}{6}$”是$tan({π-a})=-\frac{{\sqrt{3}}}{3}$的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
20.$\frac{-2+5i}{6-3i}$=( )
| A. | $\frac{9}{15}-\frac{8}{15}i$ | B. | $\frac{9}{15}+\frac{8}{15}i$ | C. | $-\frac{9}{15}-\frac{8}{15}i$ | D. | $-\frac{9}{15}+\frac{8}{15}i$ |
18.函数$y=\sqrt{-{x^2}-2x+3}$的增区间是( )
| A. | [-3,-1] | B. | [-1,1] | C. | (-∞,-3] | D. | [-1,+∞) |