题目内容
下列四个函数中，既是（0，
）上的增函数，又是以π为周期的偶函数的是（ ）
| π |
| 2 |
| A、y=tanx |
| B、y=|sinx| |
| C、y=cosx |
| D、y=|cosx| |
考点：正弦函数的图象,余弦函数的图象
专题：三角函数的图像与性质
分析：根据函数单调性，周期性和奇偶性分别进行判断即可得到结论．
解答：
解：A．函数y=tanx为奇函数，不满足条件．
B．函数y=|sinx|满足既是（0，
）上的增函数，又是以π为周期的偶函数．
C．y=cosx的周期为2π，不满足条件．
D．y=|cosx|在（0，
）上是减函数，不满足条件．
故选：B．
B．函数y=|sinx|满足既是（0，
| π |
| 2 |
C．y=cosx的周期为2π，不满足条件．
D．y=|cosx|在（0，
| π |
| 2 |
故选：B．
点评：本题主要考查三角函数的图象和性质，要求熟练掌握三角函数的周期性，奇偶性和单调性．
练习册系列答案
相关题目
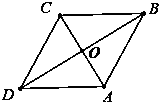
如图，在菱形ABCD中，∠DAB=120°，则以下说法错误的是（ ）
A、与
| ||||||
B、与
| ||||||
C、
| ||||||
D、
|
已知△ABC的顶点A（0，0），B（4，0），且AC边上的中线BD的长为3，则顶点C的轨迹方程是（ ）
| A、（x-8）2+y2=36（y≠0） |
| B、（x-4）2+y2=9（y≠0） |
| C、x2+y2=9（y≠0） |
| D、3x+4y-12=0（y≠0） |
圆（x+2）2+（y+1）2=4关于x轴对称的圆的方程为（ ）
| A、（x-2）2+（y+1）2=4 |
| B、（x+2）2+（y-1）2=4 |
| C、（x-2）2+（y-1）2=4 |
| D、（x+2）2+（y+1）2=4 |
1426和1643的最大公约数是（ ）
| A、34 | B、12 | C、93 | D、31 |
若正实数x，y满足x+y=2，且
≥M恒成立，则M的最大值为（ ）
| 1 |
| xy |
| A、1 | B、2 | C、3 | D、4 |
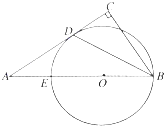如图，在Rt△ABC中，∠C=90°，E为AB上一点，以BE为直径作圆O与AC相切于点D．若AB：BC=2：1，CD=