题目内容
正方体AC1中,点P、Q分别为棱A1B1、DD1的中点,则PQ与AC1所成的角为( )
| A、30° | B、45° |
| C、60° | D、90° |
考点:异面直线及其所成的角
专题:计算题,空间角
分析:建立坐标系,设正方体的棱长为2,证明
•
=0,即可求出PQ与AC1所成的角.
| PQ |
| AC1 |
解答:
 解:建立如图所示的坐标系,设正方体的棱长为2,则
解:建立如图所示的坐标系,设正方体的棱长为2,则
A(2,0,0),C1(0,2,2),Q(0,0,1),P(2,1,2),
∴
=(-2,-1,-1),
=(-2,2,2),
∴
•
=0,
∴
⊥
,
∴PQ与AC1所成的角为90°.
故选:D.
 解:建立如图所示的坐标系,设正方体的棱长为2,则
解:建立如图所示的坐标系,设正方体的棱长为2,则A(2,0,0),C1(0,2,2),Q(0,0,1),P(2,1,2),
∴
| PQ |
| AC1 |
∴
| PQ |
| AC1 |
∴
| PQ |
| AC1 |
∴PQ与AC1所成的角为90°.
故选:D.
点评:本题考查异面直线及其所成的角,考查向量法的运用,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设M是△ABC所在平面上的一点,且
+
+
=
,D是AC中点,则
的值为( )
| MB |
| 3 |
| 2 |
| MA |
| 3 |
| 2 |
| MC |
| 0 |
|
| ||
| |BM| |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
动点P到点A(8,0)的距离是到点B(2,0)的距离的2倍,则动点P的轨迹方程为( )
| A、x2+y2=32 |
| B、x2+y2=16 |
| C、(x-1)2+y2=16 |
| D、x2+(y-1)2=16 |
设α是第二象限角,P(x,4)为其终边上的一点,且cosα=
x,则tanα等于( )
| 1 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
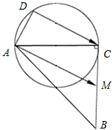 如图,已知:|AC|=|BC|=2,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则
如图,已知:|AC|=|BC|=2,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则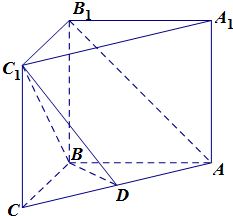 如图,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ABC=
如图,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ABC=