题目内容
设M是△ABC所在平面上的一点，且
+
+
=
，D是AC中点，则
的值为（ ）
| MB |
| 3 |
| 2 |
| MA |
| 3 |
| 2 |
| MC |
| 0 |
|
| ||
| |BM| |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：结合题意，画出图形，利用图形，延长MD至E，使DE=MD，得到平行四边形MAEC，求出
与
的关系，即可得出正确的结论．
| MD |
| MB |
解答：
解：如图所示，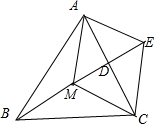
∵D是AC之中点，延长MD至E，使得DE=MD，
∴四边形MAEC为平行四边形，
∴
=
=
（
+
）；
又∵
+
+
=
，
∴
=-
（
+
）=-3
；
∴
=
=
．
故选：A．
∵D是AC之中点，延长MD至E，使得DE=MD，
∴四边形MAEC为平行四边形，
∴
| MD |
| 1 |
| 2 |
| ME |
| 1 |
| 2 |
| MA |
| MC |
又∵
| MB |
| 3 |
| 2 |
| MA |
| 3 |
| 2 |
| MC |
| 0 |
∴
| MB |
| 3 |
| 2 |
| MA |
| MC |
| MD |
∴
|
| ||
|
|
|
| ||
|-3
|
| 1 |
| 3 |
故选：A．
点评：本题考查了平面向量的应用问题，解题时应根据题意画出图形，结合图形解答问题，解题的关键是画出平行四边形MAEC，得出
与
的关系．
| MD |
| MB |
练习册系列答案
名校课堂系列答案
相关题目
已知直线l：3x-y+6=0，则直线l在x轴上的截距是（ ）
| A、1 | ||||
| B、-1 | ||||
C、
| ||||
| D、-2 |
已知|正方体AC1中，点P、Q分别为棱A1B1、DD1的中点，则PQ与AC1所成的角为（ ）
| A、30° | B、45° |
| C、60° | D、90° |