Question

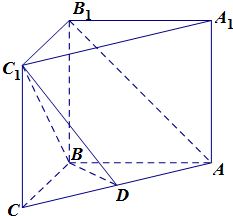如图，在三棱柱ABC-A₁B₁C₁中，侧棱A₁A⊥底面ABC，∠ABC=

π

2

，D是棱AC的中点，且AB=BC=BB₁=2．
（Ⅰ）求证：AB₁∥平面BC₁D；
（Ⅱ）求异面直线AB₁与BC₁所成的角．

Answer 1

考点：直线与平面平行的判定,异面直线及其所成的角

专题：综合题,空间位置关系与距离,空间角

分析：（Ⅰ）连结CB₁交BC₁于点O，利用三角形中位线的性质证明AB₁∥OD，即可证明AB₁∥平面BC₁D；
（Ⅱ）确定∠DOB为异面直线AB₁与BC₁所成的角或其补角，再求异面直线AB₁与BC₁所成的角．

解答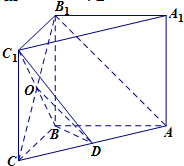： （Ⅰ）证明：连结CB₁交BC₁于点O，
∵侧棱AA₁⊥底面ABC，∴侧面BB₁C₁C是矩形，
∴O为B₁C的中点，且D是棱AC的中点，∴AB₁∥OD，…（4分）
∵OD?平面BC₁D，AB₁?平面BC₁D，
∴AB₁∥平面BC₁D                            …（6分）
（Ⅱ）解：∵AB₁∥OD，∴∠DOB为异面直线AB₁与BC₁所成的角或其补角．…（8分）
∵∠ABC=

π

2

，AB=BC=BB₁=2，
∴BD=

2

，OD=

2

，OB=

2

，
∴△OBD为等边三角形，∴∠DOB=60°，
∴异面直线AB₁与BC₁所成的角为60°．…（12分）

点评：本题考查线面平行，考查线线角，考查学生分析解决问题的能力，解题的关键是正确运用线面平行的判定定理．