题目内容
设α是第二象限角,P(x,4)为其终边上的一点,且cosα=
x,则tanα等于( )
| 1 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
考点:任意角的三角函数的定义
专题:三角函数的求值
分析:依题意,可得cosα=
=
x,可求得x的值,利用正切函数的定义即可得到答案.
| x | ||
|
| 1 |
| 5 |
解答:
解:∵cosα=
=
x,
∴
=5,解得x=±3,
又α是第二象限角,
∴x=-3,
∴tanα=
=-
,
故选:A.
| x | ||
|
| 1 |
| 5 |
∴
| x2+16 |
又α是第二象限角,
∴x=-3,
∴tanα=
| 4 |
| -3 |
| 4 |
| 3 |
故选:A.
点评:本题考查任意角的三角函数的定义,求得x的值是关键,属于基础题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
正方体AC1中,点P、Q分别为棱A1B1、DD1的中点,则PQ与AC1所成的角为( )
| A、30° | B、45° |
| C、60° | D、90° |
若定义在[-2014,2014]上的函数f(x)满足:对于任意的x1,x2∈[-2014,2014],有f(x1+x2)=f(x1)+f(x2)-2013,且x>0时,有f(x)>2013,f(x)的最大、小值分别为M、N,则M+N的值为( )
| A、4026 | B、4028 |
| C、2013 | D、2014 |
p为椭圆
+
=1上的一点,F1,F2分别为左、右焦点,且∠F1PF2=60° 则|PF1|•|PF2|=( )
| x2 |
| 9 |
| y2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=log2
•log
(2x)的最小值为( )
| x |
| 2 |
| A、0 | ||
B、-
| ||
C、-
| ||
D、
|
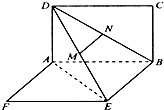 如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1,线段AB的长为
如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1,线段AB的长为