题目内容
双曲线
-
=1(a>0,b>0)的左右焦点分别为F1,F2,过焦点F2与x轴垂直的直线与双曲线交于P,Q两点,若△PF1Q是等边三角形,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、2
| ||
C、
| ||
D、2
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:首先,将点P(c,y0)代入双曲线
-
=1得到:y0=
由△PF1Q是等边三角形所以:
=
进一步解得:
b2=2ac所以
(c2-a2)=2ac所以整理得:
e2-2e-
=0解得离心率.
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
| |F1F2| |
| |PF2| |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
解答:
解:不妨设P(c,y0)其中y0>0,c为双曲线的半焦距,将点P(c,y0)代入双曲线
-
=1得到:y0=
由△PF1Q是等边三角形
所以:
=
进一步解得:
b2=2ac
所以
(c2-a2)=2ac所以整理得:
e2-2e-
=0
解得:e=
或-
(负值舍去)
故选:A
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
所以:
| |F1F2| |
| |PF2| |
| 3 |
| 3 |
所以
| 3 |
| 3 |
| 3 |
解得:e=
| 3 |
| ||
| 3 |
故选:A
点评:本题考查的知识要点:等边三角形的边角关系,双曲线的离心率及相关的运算问题.

练习册系列答案
相关题目
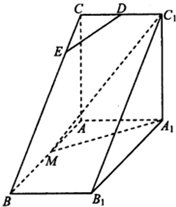 如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.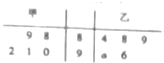 某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0-9的某个整数
某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0-9的某个整数