题目内容
已知椭圆C的焦点在x轴上,短轴长和焦距均为2.
(1)求椭圆C的标准方程及离心率;
(2)设O为原点.若点A在直线y=2上,点B在椭圆C上,且OA⊥OB,求线段AB长度的最小值.
(1)求椭圆C的标准方程及离心率;
(2)设O为原点.若点A在直线y=2上,点B在椭圆C上,且OA⊥OB,求线段AB长度的最小值.
考点:直线与圆锥曲线的关系,椭圆的标准方程,椭圆的简单性质
专题:圆锥曲线中的最值与范围问题
分析:(1)设椭圆方程为:
+
=1,由题意可求2c,2b,然后由a2=b2+c2可求a,进而可求椭圆C方程;
(2)由题意设点A,B的坐标分别为(t,2),(x0,y0),可得|AB|2=(x0-t)2+(y0-2)2=(x0+
)2+(y0-2)2=
+
+3,利用基本不等式求最值即可.
| x2 |
| a2 |
| y2 |
| b2 |
(2)由题意设点A,B的坐标分别为(t,2),(x0,y0),可得|AB|2=(x0-t)2+(y0-2)2=(x0+
| 2y0 |
| x0 |
| ||
| 2 |
| 4 | ||
|
解答:
解析 (1)由题意知,2c=2,2b=2,∴c=1,b=1,
∴c2=1,b2=1,从而a2=c2+b2=2.∴a=
,
∴椭圆C的标准方程为
+y2=1,椭圆C的离心率e=
.
(2)设点A,B的坐标分别为(t,2),(x0,y0),其中x0≠0.
因为OA⊥OB,所以
•
=0,即tx0+2y0=0,解得t=-
.
又
+2
=2,
所以|AB|2=(x0-t)2+(y0-2)2
=(x0+
)2+(y0-2)2
=
+
+3,
≥2
+3.
当且仅当x0=2时,等号成立,
所以|AB|≥
+1.
故线段AB长度的最小值为
+1.
∴c2=1,b2=1,从而a2=c2+b2=2.∴a=
| 2 |
∴椭圆C的标准方程为
| x2 |
| 2 |
| ||
| 2 |
(2)设点A,B的坐标分别为(t,2),(x0,y0),其中x0≠0.
因为OA⊥OB,所以
| OA |
| OB |
| 2y0 |
| x0 |
又
| x | 2 0 |
| y | 2 0 |
所以|AB|2=(x0-t)2+(y0-2)2
=(x0+
| 2y0 |
| x0 |
=
| ||
| 2 |
| 4 | ||
|
≥2
| 2 |
当且仅当x0=2时,等号成立,
所以|AB|≥
| 2 |
故线段AB长度的最小值为
| 2 |
点评:本题主要考查了利用椭圆的性质求解椭圆方程,直线与椭圆的相交关系的应用,属于中档试题

练习册系列答案
相关题目
如图执行下面的流程图,那么输出的S等于( )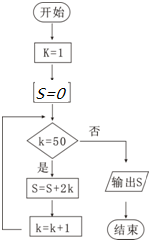

| A、2450 | B、2500 |
| C、2550 | D、2652 |
 如图,AB是圆O的直径,C是圆周上不同于A,B的任意一点,PA⊥平面ABC,则四面体P-ABC的四个面中,直角三角形的个数有
如图,AB是圆O的直径,C是圆周上不同于A,B的任意一点,PA⊥平面ABC,则四面体P-ABC的四个面中,直角三角形的个数有