题目内容
设函数y=x2+(a+1)2+|x+a-1|(a∈R).
(1)若a为大于2的常数,求函数y的最小值;
(2)若函数y的最小值大于3,求实数a的取值范围.
(1)若a为大于2的常数,求函数y的最小值;
(2)若函数y的最小值大于3,求实数a的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)先去掉绝对值,分别求函数的最小值,然后比较大小即可得函数的最小值;
(2)像(1)一样分别让最小值大于3,求实数a的取值范围即可.
(2)像(1)一样分别让最小值大于3,求实数a的取值范围即可.
解答:
解:(1)设f(x)=y=x2+(a+1)2+|x+a-1|=
,
因为a>2,所以1-a<-1,
当x>1-a时,ymin=f(-
)=(a+1)2+a-
,
当x≤1-a时,ymin=f(1-a)=2+2a2,
又2+2a2-[(a+1)2+a-
]=(a-
)2≥0,
∴2+2a2≥(a+1)2+a-
,
∴a为大于2的常数,函数y的最小值为(a+1)2+a-
,
(2)设f(x)=y=x2+(a+1)2+|x+a-1|=
,
∴当x≥1-a时,即x=-
,此时a≥
,ymin=f(-
)=(a+1)2+a-
>3,解得:a<-
或a>
;
∴a≥
,
当x<1-a时,即x<1-a,此时a<
,ymin=f(
)=(a+1)2-a+
>3,解得:a<-
或a>
,
∴a<-
综上:a<-
或a≥
.
|
因为a>2,所以1-a<-1,
当x>1-a时,ymin=f(-
| 1 |
| 2 |
| 5 |
| 4 |
当x≤1-a时,ymin=f(1-a)=2+2a2,
又2+2a2-[(a+1)2+a-
| 5 |
| 4 |
| 3 |
| 2 |
∴2+2a2≥(a+1)2+a-
| 5 |
| 4 |
∴a为大于2的常数,函数y的最小值为(a+1)2+a-
| 5 |
| 4 |
(2)设f(x)=y=x2+(a+1)2+|x+a-1|=
|
∴当x≥1-a时,即x=-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
3+
| ||
| 2 |
-3+
| ||
| 2 |
∴a≥
| 3 |
| 2 |
当x<1-a时,即x<1-a,此时a<
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
1+
| ||
| 2 |
-1+
| ||
| 2 |
∴a<-
1+
| ||
| 2 |
综上:a<-
1+
| ||
| 2 |
| 3 |
| 2 |
点评:本题主要考查二次函数的最值问题,借助二次函数的对称性和单调性求解.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是( )
A、y=
| ||
| B、y=e-x | ||
| C、y=-x2+1 | ||
| D、y=lg|x| |
已知
+
=2
,且
=2
,若∠A=120°,
•
=-3,则|
|的最小值为( )
| AB |
| AC |
| AQ |
| AP |
| PQ |
| AB |
| AC |
| AP |
| A、3 | ||||
B、
| ||||
C、
| ||||
| D、2 |
如图执行下面的流程图,那么输出的S等于( )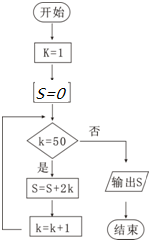

| A、2450 | B、2500 |
| C、2550 | D、2652 |