题目内容
已知函数f(x)=ex-kx,(k∈R,x∈R)
(1)当k=e时.求函数f(x)的极小值;
(2)若k>0,且对于任意x≥0总有f(x)>0恒成立.求实数k的取值范围;
(3)令g(x)=ex-3lnx,若至少存在一个实数x0∈[1,e],使f(x0)<g(x0)成立.求实数k的取值范围.
(1)当k=e时.求函数f(x)的极小值;
(2)若k>0,且对于任意x≥0总有f(x)>0恒成立.求实数k的取值范围;
(3)令g(x)=ex-3lnx,若至少存在一个实数x0∈[1,e],使f(x0)<g(x0)成立.求实数k的取值范围.
考点:利用导数研究函数的极值,利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)将k=e代入函数的表达式,通过求导得到函数的单调区间,进而求出函数的极小值;
(2)先求出函数的导数,将问题转化为求f(x)的最小值大于0,解不等式,求出即可;
(3)将问题转化为求两个函数的最值问题,画出函数的图象,结合函数的单调性,容易得到答案.
(2)先求出函数的导数,将问题转化为求f(x)的最小值大于0,解不等式,求出即可;
(3)将问题转化为求两个函数的最值问题,画出函数的图象,结合函数的单调性,容易得到答案.
解答:
解:(1)k=e时,f(x)=ex-ex,f′(x)=ex-e,
令f′(x)>0,解得:x>1,令f′(x)<0,解得:x<1,
∴f(x)在(-∞,1)递减,在(1,+∞)递增,
∴f(x)min=f(1)=0;
(2)∵f′(x)=ex-k,k>0
令f′(x)>0,解得:x>lnk,令f′(x)<0,解得:x<lnk,
∴f(x)在[0,lnk)递减,在(lnk,+∞)递增,
∴f(x)min=f(lnk)=k-klnk>0,解得:0<k<e,
(3)若f(x)<g(x),则ex-kx<ex-3lnx,
∴lnx<
x,
令m(x)=lnx,n(x)=
x,
画出函数m(x),n(x)的图象,如图示:
 ,
,
由题意得:只需m(x)的最小值小于g(x)的最大值即可,
∴0<
,解得:k>0,
令f′(x)>0,解得:x>1,令f′(x)<0,解得:x<1,
∴f(x)在(-∞,1)递减,在(1,+∞)递增,
∴f(x)min=f(1)=0;
(2)∵f′(x)=ex-k,k>0
令f′(x)>0,解得:x>lnk,令f′(x)<0,解得:x<lnk,
∴f(x)在[0,lnk)递减,在(lnk,+∞)递增,
∴f(x)min=f(lnk)=k-klnk>0,解得:0<k<e,
(3)若f(x)<g(x),则ex-kx<ex-3lnx,
∴lnx<
| k |
| 3 |
令m(x)=lnx,n(x)=
| k |
| 3 |
画出函数m(x),n(x)的图象,如图示:
 ,
,由题意得:只需m(x)的最小值小于g(x)的最大值即可,
∴0<
| ke |
| 3 |
点评:本题考查了函数的单调性,函数的最值问题,考查了导数的应用,考查转化思想,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知集合B={2,3,4},那么B的真子集的个数是( )
| A、15 | B、16 | C、7 | D、8 |
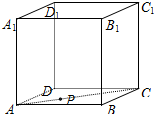 如图,在正方体ABCD-A1B1C1D1中,点P在面对角线AC上运动,给出下列命题:
如图,在正方体ABCD-A1B1C1D1中,点P在面对角线AC上运动,给出下列命题: 如图,已知ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面BCME.
如图,已知ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面BCME.