题目内容
给出下列四个命题:
①?x∈R,x2≥x;
②?x∈R,x2≥x;
③命题:“若P则?q”的否命题是:“若P则q”
④“x2≠1”的充要条件是“x≠1,或x≠-1”
其中正确命题的个数是( )
①?x∈R,x2≥x;
②?x∈R,x2≥x;
③命题:“若P则?q”的否命题是:“若P则q”
④“x2≠1”的充要条件是“x≠1,或x≠-1”
其中正确命题的个数是( )
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:①取x=
,则(
)2=
<
,由此可判断①;
②?x=1∈R,使得12≥1成立,可判断②;
③写出“若P则¬q”的否命题,可判断③;
④分析可得“x2≠1”的充要条件是“x≠1,且x≠-1”,从而可判断④.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
②?x=1∈R,使得12≥1成立,可判断②;
③写出“若P则¬q”的否命题,可判断③;
④分析可得“x2≠1”的充要条件是“x≠1,且x≠-1”,从而可判断④.
解答:
解:①?x∈R,x2≥x,错误,如x=
时,(
)2=
<
,故①错误;
②?x=1∈R,使得12≥1成立,故②正确;
③命题:“若P则¬q”的否命题是:“若¬P则q”,而不是“若P则q”,故③错误;
④若x2≠1,则x≠1,且x≠-1,充分性成立;反之,若x≠1,且x≠-1,则x2≠1,即必要性成立;
故“x2≠1”的充要条件是“x≠1,且x≠-1”,而不是“x≠1,或x≠-1”,故④错误;
综上,正确命题的个数是1个.
故选:B.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
②?x=1∈R,使得12≥1成立,故②正确;
③命题:“若P则¬q”的否命题是:“若¬P则q”,而不是“若P则q”,故③错误;
④若x2≠1,则x≠1,且x≠-1,充分性成立;反之,若x≠1,且x≠-1,则x2≠1,即必要性成立;
故“x2≠1”的充要条件是“x≠1,且x≠-1”,而不是“x≠1,或x≠-1”,故④错误;
综上,正确命题的个数是1个.
故选:B.
点评:本题考查命题的真假判断与应用,着重考查全称命题与特称命题的概念及应用,考查充分、必要条件及命题间的关系,属于中档题.

练习册系列答案
相关题目
在△ABC中,若cosA•cosB=sinA•sinB,则△ABC为( )
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、无法确定 |
一个正四棱锥的五个顶点都在半径为1的球面上,其中底面的四个顶点在该球的一个大圆上,则该正四棱锥的体积是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
(理)已知
=a,且函数 f(x)=aebx-cx有大于0的极点值,则实数b的取值范围是( )
| lim |
| x→2 |
| x2+cx+2 |
| x-2 |
| A、(-∞,-3) | ||
| B、(-3,+∞) | ||
C、(-∞,-
| ||
D、(-
|
一个算法的程序框图如图所示,若该程度输出的结果为
,则判断框①中应填入的条件是( )

| 7 |
| 12 |

| A、i<5 | B、i<4 |
| C、i>4 | D、i≤3 |
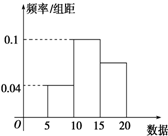 如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数与中位数分别为( )
如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数与中位数分别为( )| A、10 13 |
| B、12.5 12 |
| C、12.5 13 |
| D、10 15 |
已知函数f(x)是R上的偶函数,且在(0,+∞)上单调递减,则f(a2-2a+3)与f(-2)的大小关系为( )
| A、f(a2-2a+3)>f(-2) |
| B、f(a2-2a+3)<f(-2) |
| C、f(a2-2a+3)≥f(-2) |
| D、f(a2-2a+3)≤f(-2) |
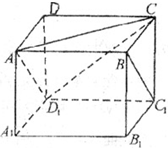 如图,正方体ABCD-A1B1C1D1,则下列四个命题:
如图,正方体ABCD-A1B1C1D1,则下列四个命题: