题目内容
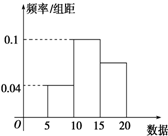如图所示是一样本的频率分布直方图，则由图形中的数据，可以估计众数与中位数分别为（ ）| A、10 13 |
| B、12.5 12 |
| C、12.5 13 |
| D、10 15 |
考点：频率分布直方图,众数、中位数、平均数
专题：概率与统计
分析：根据众数是频率分布直方图中最高矩形的底边中点的横坐标，中位数是把频率分布直方图分成两个面积相等部分的平行于Y轴的直线横坐标进行解题即可．
解答：
解：众数是频率分布直方图中最高矩形的底边中点的横坐标，
∴中间的一个矩形最高，故10与15的中点是12.5，众数是12.5
而中位数是把频率分布直方图分成两个面积相等部分的平行于Y轴的直线横坐标
第一个矩形的面积是0.2，第三个矩形的面积是0.3，故将第二个矩形分成3：2即可
∴中位数是13
故选：C．
∴中间的一个矩形最高，故10与15的中点是12.5，众数是12.5
而中位数是把频率分布直方图分成两个面积相等部分的平行于Y轴的直线横坐标
第一个矩形的面积是0.2，第三个矩形的面积是0.3，故将第二个矩形分成3：2即可
∴中位数是13
故选：C．
点评：用样本估计总体，是研究统计问题的一个基本思想方法．频率分布直方图中小长方形的面积=组距×
=频率，各个矩形面积之和等于1，能根据直方图求众数和中位数，属于常规题型．
| 频率 |
| 组距 |
练习册系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
若0＜α＜
＜β＜π，且cosβ=-
，sin（α+β）=
，则sinα的值是（ ）
| π |
| 2 |
| 1 |
| 3 |
| 7 |
| 9 |
A、
| ||
B、
| ||
C、
| ||
D、
|
给出下列四个命题：
①?x∈R，x2≥x；
②?x∈R，x2≥x；
③命题：“若P则?q”的否命题是：“若P则q”
④“x2≠1”的充要条件是“x≠1，或x≠-1”
其中正确命题的个数是（ ）
①?x∈R，x2≥x；
②?x∈R，x2≥x；
③命题：“若P则?q”的否命题是：“若P则q”
④“x2≠1”的充要条件是“x≠1，或x≠-1”
其中正确命题的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
已知0＜α＜
＜β＜π，cos（α-β）=
，sinβ=
，则sinα=（ ）
| π |
| 2 |
| 4 |
| 5 |
| ||
| 10 |
A、
| ||||
B、±
| ||||
C、-
| ||||
D、-
|
在等差数列{an}中，2a8+a9+a15=20，则数列{an}的前19项之和为（ ）
| A、98 | B、95 | C、93 | D、90 |
若复数
（a∈R，i是虚数单位）为纯虚数，则a=（ ）
| 1+ai |
| 2+i |
| A、2 | B、-2 | C、1 | D、-1 |
函数y=ex-x-2的单调递减区间是（ ）
| A、（-∞，0） |
| B、（0，+∞） |
| C、（-∞，1） |
| D、（-1，+∞） |
若直线l过点P（1，0）与双曲线x2-
=1只有一个公共点，则这样的直线有（ ）
| y2 |
| 4 |
| A、4条 | B、3条 | C、2条 | D、1条 |
直线（m+2）x+（2-m）y=2m在x轴上的截距为3，则m的值是（ ）
A、
| ||
B、-
| ||
| C、6 | ||
| D、-6 |