题目内容

如图1，已知正方形ABCD，E、F分别是AB、CD中点，将△ADE沿DE折起，如图2示，求证：BF∥平面ADE．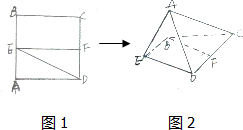
考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：根据直线与平面平行的判定定理可知，只要在平面ADE内找到与直线BF平行的直线就可以了，易证四边形EBFD为平行四边形；
解答： 证明：EF分别为正方形ABCD得边AB、CD的中点，
∵EB∥FD，且EB=FD，
∴四边形EBFD为平行四边形．
∴BF∥ED
∵EF?平面AED，而BF?平面AED，
∴BF∥平面ADE．
点评：本题考查了空间中的线面平行的判定，关键是正确利用线面平行的判定定理．
练习册系列答案
相关题目
向量
a
=(2，sinθ)，
b
=(1，cosθ)，θ为锐角，若
a
∥
b
，则tan2θ的值为
 
．
下面有五个命题
①函数f（x）=sin4x-cos4x图象的一个对称中心是(-
π
4
，0)；
②y=
x+3
x-1
的图象关于点（-1，1）对称，
③定义在R上的偶函数f（x）满足f（x+2）=-f（x），且在[-6，-4]上是增函数，在锐角△ABC中，令m=f（sinA+sinB），n=f（cosA+cosC），则m和n的大小关系为m＞n
④设f（x）是连续的偶函数，且在（0，+∞）是单调函数，则方程f(x)=f(
x+3
x+4
)所有根之和为8
⑤不等式sinx＞
4x2
π2
对任意x∈(0，
π
2
)恒成立．
其中真命题的序号是
 
．
在实数集R中，我们定义的大小关系“＞”为全体实数排了一个“序”，类似的，我们在平面向量集D={
a
|
a
=（x，y），x∈R，y∈R}上也可以定义一个称为“序”的关系，记为“＞”．定义如下：对于任意两个向量
a1
=（x1，y1），
a2
=（x2，y2），
a1
＞
a2
当且仅当“x1＞x2”或“x1=x2且y1＞y2”按上述定义的关系“＞”，给出下列四个命题：
①若
e1
=（1，0），
e2
=（0，1），
0
=（0，0）则
e1
＞
e2
＞
0
；
②若
a1
＞
a2
，
a2
＞
a3
，则
a1
＞
a3
；
③若
a1
＞
a2
，则对于任意
a
∈D，
a1
+
a
＞
a2
+
a
；
④对于任意向量
a
＞
0
，
0
=(0，0)，若
a1
＞
a2
，则
a
•
a1
＞
a
•
a2
．
其中命题正确的序号为（　　）
A、①②B、①③
C、①②③D、①②③④
已知函数f（x）=2x3-ax2+6在x=1时取得极值
（1）求a的值，并求函数f（x）的单调区间；
（2）求函数f（x）的极大值和极小值．
下列命题为真命题的是
 
．（用序号表示即可）
①cos1＞cos2＞cos3；
②若an=an+3且an=n+3（n=1、2、3），则a2013＜a2014＜a2015；
③若e1、e2、e3分别为双曲线x2-
y2
3
=1、
x2
4
-
y2
3
=1、
x2
4
-y2=1的离心率，则e1＞e2＞e3；
④若x1＞x2＞x3，则lgx1＞lgx2＞lgx3．
已知双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的离心率e=
2
3
3
，经过A（a，0），B（0，-b）两点的直线l与原点的距离d=
3
2

（1）求双曲线C的方程；
（2）直线y=kx+5与双曲线C交于M，N两点，若|BM|=|BN|，求斜率k的值．
已知正四棱柱的底面边长为4cm，高为5cm，求它的全面积和体积．
已知函数y=Asin（ωx+φ），（A＞0，ω＞0，|φ|＜
π
2
）相邻的最高点和最低点分别为（
π
6
，2），（
2π
3
，-2）．求函数表达式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网