题目内容
已知函数f(x)=2x3-ax2+6在x=1时取得极值
(1)求a的值,并求函数f(x)的单调区间;
(2)求函数f(x)的极大值和极小值.
(1)求a的值,并求函数f(x)的单调区间;
(2)求函数f(x)的极大值和极小值.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:计算题,导数的概念及应用
分析:(1)先求出导数f′(x)=6x2-2ax,由f′(1)=0得a=3,令f′(x)>0得出函数的增区间,令f′(x)<0得出函数的减区间;
(2)由(1)得:x=0时函数取得极大值,x=1时函数取得极小值,直接代入函数的解析式求出极值即可.
(2)由(1)得:x=0时函数取得极大值,x=1时函数取得极小值,直接代入函数的解析式求出极值即可.
解答:
解:(1)f′(x)=6x2-2ax
又∵f′(1)=0,∴a=3
则f(x)=2x3-3x2+6
∴f′(x)=6x2-6x
令f′(x)>0即6x2-6x>0 得x<0 或x>1
令f′(x)<0即6x2-6x<0 得0<x<1
∴函数f(x)的单调增区间为:(-∞,0)和(1,+∞),
函数f(x)的单调减区间为:(0,1)
(2)由(1)得:x=0时函数取得极大值,x=1时函数取得极小值,
则函数f(x)极大值=f(0)=6
函数f(x)极大值=f(1)=5.
又∵f′(1)=0,∴a=3
则f(x)=2x3-3x2+6
∴f′(x)=6x2-6x
令f′(x)>0即6x2-6x>0 得x<0 或x>1
令f′(x)<0即6x2-6x<0 得0<x<1
∴函数f(x)的单调增区间为:(-∞,0)和(1,+∞),
函数f(x)的单调减区间为:(0,1)
(2)由(1)得:x=0时函数取得极大值,x=1时函数取得极小值,
则函数f(x)极大值=f(0)=6
函数f(x)极大值=f(1)=5.
点评:本题主要考查了函数的极值问题及导数的应用,利用导数作为工具去研究函数的性质非常方便.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
已知集合A={x|0<x<2},集合B={x|1<x≤3},则A∪B=( )
| A、A={x|0<x<3} |
| B、B={x|0<x≤3} |
| C、B={x|1<x<2} |
| D、B={x|0<x<3} |
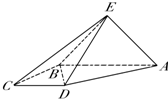 如图,四棱锥E-ABCD中,面ABE⊥面ABCD,侧面ABE是等腰直角三角形,EA⊥EB,且AB∥CD,AB⊥BC,AB=2CD=2BC=2.
如图,四棱锥E-ABCD中,面ABE⊥面ABCD,侧面ABE是等腰直角三角形,EA⊥EB,且AB∥CD,AB⊥BC,AB=2CD=2BC=2.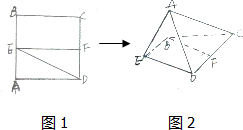
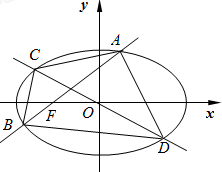 如图,已知椭圆E:
如图,已知椭圆E: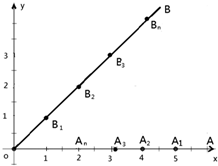 平面直角坐标系中,O为原点,射线OA与x轴正半轴重合,射线OB是第一象限角平分线.在OA上有点列A1,A2,A3,…,An,…,在OB上有点列B1,B2,B3,…,Bn,…已知
平面直角坐标系中,O为原点,射线OA与x轴正半轴重合,射线OB是第一象限角平分线.在OA上有点列A1,A2,A3,…,An,…,在OB上有点列B1,B2,B3,…,Bn,…已知