题目内容
已知函数y=Asin(ωx+φ),(A>0,ω>0,|φ|<
)相邻的最高点和最低点分别为(
,2),(
,-2).求函数表达式.
| π |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:解:由函数图象过最高点的坐标可得A=2,相邻的最值点的横坐标为半个周期,得T=π,又T=
,可得ω=2;当x=
时,y=2,得
+φ=
+2kπ,k∈Z,由|φ|<
得:φ=
,于是可得答案.
| 2π |
| ω |
| π |
| 6 |
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
解答:
解:由函数图象过最高点的坐标可得A=2,
相邻的最值点的横坐标为半个周期,即
=
-
=
,得T=π,又T=
,
所以ω=2.
所以y=2sin(2x+φ),当x=
时,y=2,得2sin(2×
+φ)=2,即sin(
+φ)=1,
所以
+φ=
+2kπ,k∈Z,
由|φ|<
得:φ=
,
所以y=sin(2x+
).
相邻的最值点的横坐标为半个周期,即
| T |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| 2π |
| ω |
所以ω=2.
所以y=2sin(2x+φ),当x=
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
所以
| π |
| 3 |
| π |
| 2 |
由|φ|<
| π |
| 2 |
| π |
| 6 |
所以y=sin(2x+
| π |
| 6 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,求φ是难点,考查转化思想与运算能力.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
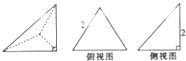 已知三棱锥的直观图及其俯视图与侧视图如图,俯视图是边长为2的正三角形,侧视图是有一直角边为2的直角三角形,则该三棱锥的正视图面积为( )
已知三棱锥的直观图及其俯视图与侧视图如图,俯视图是边长为2的正三角形,侧视图是有一直角边为2的直角三角形,则该三棱锥的正视图面积为( )