题目内容
方程
+
=1表示一个椭圆时,求m的取值范围.
| x2 |
| 25-m |
| y2 |
| 16-m |
考点:二元二次方程表示圆的条件
专题:直线与圆
分析:本题可根据椭圆的方程的特征,得到参数满足的条件,解相应关系式,得到本题结论.
解答:
解:∵方程
+
=1表示一个椭圆时,
∴25-m>0,16-m>0,25-m≠16-m,
∴m<16.
∴m的取值范围为:(-∞,16).
| x2 |
| 25-m |
| y2 |
| 16-m |
∴25-m>0,16-m>0,25-m≠16-m,
∴m<16.
∴m的取值范围为:(-∞,16).
点评:本题考查了椭圆的方程的特征,本题难度不大,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设x,y满足约束条件
,若x2+y2≥a恒成立,则实数a的最大值为( )
|
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
已知函数:f(x)=x2-4|x|+1,若关于x的方程:f(x)=2k恰有四个不等的实数根,则实数k的取值范围为( )
A、-
| ||||
| B、-3<k<1 | ||||
| C、-6<k<2 | ||||
D、k>-
|
已知f(x)=sin(2014x+
)+cos(2014x-
)的最大值为A,若存在实数x1,x2,使得对任意实数x总有f(x1)≤f(x)≤f(x2)成立,则A|x1-x2|的最小值为( )
| π |
| 6 |
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
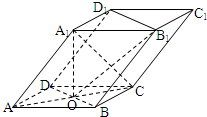 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=