题目内容
从集合{1,2,3,…,n}的所有非空子集中等可能的取出一个.
(Ⅰ)记性质t:集合中所有元素之和为m(m<n且m为偶数),求取出的是至多含有2个元素且满足性质t的非空子集的概率;
(Ⅱ)记所有取出的非空子集的元素个数为ξ,求ξ的分布列及其数学期望.
(Ⅰ)记性质t:集合中所有元素之和为m(m<n且m为偶数),求取出的是至多含有2个元素且满足性质t的非空子集的概率;
(Ⅱ)记所有取出的非空子集的元素个数为ξ,求ξ的分布列及其数学期望.
考点:离散型随机变量及其分布列,离散型随机变量的期望与方差
专题:概率与统计
分析:(I)记“所取出的非空子集满足性质r”为事件A,则基本事件数是2n-1个.分别对n分类讨论:当n=3时;当n=4时;当n=5时;当n=6时;当n=7时;当n=8时.可得:当n=2k-1或2k(k≥2)时,满足性质r的集合只有1+2+…+(k-1)=
个.即可得出:取出的是至多含有2个元素且满足性质t的非空子集的概率.
(2)由题意知ξ的可能取值是1,2,…,n,基本事件的总数是2n-1个.ξ的分布列是:P(ξ=k)=
,进而得出数学期望.
| k(k-1) |
| 2 |
(2)由题意知ξ的可能取值是1,2,…,n,基本事件的总数是2n-1个.ξ的分布列是:P(ξ=k)=
| ||
| 2n-1 |
解答:
解:(I)记“所取出的非空子集满足性质r”为事件A,则基本事件数是2n-1个.
当n=3时,{1,2,3},其中满足性质r的集合只有一个{2};
当n=4时,{1,2,3,4},其中满足性质r的集合只有一个{2};
当n=5时,{1,2,3,4,5},其中满足性质r的集合只有3个{2},{4},{1,3};
当n=6时,{1,2,3,4,5,6},其中满足性质r的集合只有3个{2},{4},{1,3};
当n=7时,{1,2,3,4,5,6,7},其中满足性质r的集合只有6个{2},{4},{6},{1,3},{1,5},
{2,4};
当n=8时,{1,2,3,4,5,6,7,8},其中满足性质r的集合只有6个{2},{4},{6},{1,3},{1,5},
{2,4}.
…,由以上可得:当n=2k-1或2k(k≥2)时,满足性质r的集合只有1+2+…+(k-1)=
个.
∴取出的是至多含有2个元素且满足性质t的非空子集的概率P=
.
(2)由题意知ξ的可能取值是1,2,…,n,基本事件的总数是2n-1个.
ξ的分布列是:
其数学期望为E(ξ)=
=
.
当n=3时,{1,2,3},其中满足性质r的集合只有一个{2};
当n=4时,{1,2,3,4},其中满足性质r的集合只有一个{2};
当n=5时,{1,2,3,4,5},其中满足性质r的集合只有3个{2},{4},{1,3};
当n=6时,{1,2,3,4,5,6},其中满足性质r的集合只有3个{2},{4},{1,3};
当n=7时,{1,2,3,4,5,6,7},其中满足性质r的集合只有6个{2},{4},{6},{1,3},{1,5},
{2,4};
当n=8时,{1,2,3,4,5,6,7,8},其中满足性质r的集合只有6个{2},{4},{6},{1,3},{1,5},
{2,4}.
…,由以上可得:当n=2k-1或2k(k≥2)时,满足性质r的集合只有1+2+…+(k-1)=
| k(k-1) |
| 2 |
∴取出的是至多含有2个元素且满足性质t的非空子集的概率P=
| k(k-1) |
| 2(2n-1) |
(2)由题意知ξ的可能取值是1,2,…,n,基本事件的总数是2n-1个.
ξ的分布列是:
| ξ | 1 | 2 | … | n | ||||||||||||
| p(ξ) |
|
| … |
|
| ||||||
| 2n-1 |
| n•2n-1 |
| 2n-1 |
点评:本题考查了集合的性质、组合数的计算公式及其性质、概率及其数学期望的计算方法,考查了推理能力、猜想能力与计算能力,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
x>1的充分不必要条件是( )
| A、x>0 | B、x≥1 |
| C、x=0 | D、x=2 |
命题“对任意的x∈R,x2+1>0”的否定是( )
| A、不存在x∈R,x2+1>0 |
| B、存在x∈R,x2+1>0 |
| C、存在x∈R,x2+1≤0 |
| D、对任意的x∈R,x2+1≤0 |
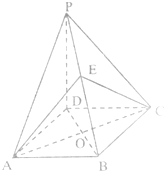 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,O为AC与BD的交点,E为PB上任意一点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,O为AC与BD的交点,E为PB上任意一点.