题目内容

若某简单空间几何体的三视图都是边长为1的正方形，则这个空间几何体的内切球的体积为（　　）
A、
4
3
π
B、
2
3
π
C、
1
3
π
D、
1
6
π
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：根据几何体的三视图是边长为1的正方形，得几何体是棱长为1的正方体，即可求出这个空间几何体的内切球的体积．
解答： 解：根据几何体的三视图是边长为1的正方形，得几何体是棱长为1的正方体，
∴几何体的内切球的体积为V=
4
3
π×（
1
2
）3=
π
6
．
故选：D．
点评：本题考查了由三视图求这个空间几何体的内切球的体积，判断几何体的形状是关键．
练习册系列答案
相关题目
已知tan（α+β）=3，tan（α-β）=5，则tan（2α）的值为（　　）
A、-
4
7
B、
4
7
C、
1
8
D、-
1
8
已知两直角边长分别为a，b的直角三角形的面积大小与其周长大小相等，则ab的最小值为
 
．
某工厂需要生产x个零件（50≤x≤150，x∈N*），经市场调查得知，生产成本包括以下三个方面：①生产1个零件需要原料费50元；②支付职工的工资由6000元的基本工资和每生产1个零件补贴20元组成；③所生产零件的保养总费用是（x2-30x+400）元．
（1）把生产每个零件的平均成本P（x）表示为x的函数关系式，并求P（x）的最小值；
（2）假设生产的零件可以全部卖出，据测算，销售收入Q（x）关于产量x的函数关系式为Q（x）=1240x-
1
30
x3，那么当产量为多少时生产这批零件的利润最大？
已知双曲线
x2
a2
-
y2
b2
=1（a＞b＞0）的其中一条渐近线的倾斜角为
π
6
，则双曲线的离心率为（　　）
A、
2
3
3
B、
2
6
3
C、
3
D、2
若l，n是两条互不相同的空间直线，α，β是两个不重合的平面，则下列命题中为真命题的是
 
（填所有正确答案的序号）．
①若α∥β，l?α，n?β，则l∥n；        
②若l⊥α，n∥α，则l⊥n；
③若α⊥β，l⊥β，则l∥α；              
④若l⊥α，l∥β，则α⊥β．
已知数列{an}中，a1=2，a2=1，
2
an
=
1
an+1
+
1
an-1
（n≥2，n∈N*），其通项公式an=
 
．
已知函数f（x）=ax+
1-x
ax
（a＞0）
（1）利用函数单调性的定义，判断函数f（x）在（0，+∞）上的单调性；
（2）求函数y=f（x）在（0，1]上的最小值g（a）
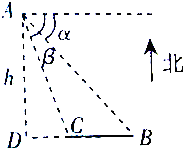如图，从气球A测得正前方的济南全运会东荷、西柳两个场馆B、C的俯角分别为α、β，此时气球的高度为h，则两个场馆B、C间的距离为（　　）
A、
hsinαsinβ
sin(α-β)
B、
hsin(β-α)
sinαsinβ
C、
hsinα
sinβsin(α-β)
D、
hsinβ
sinαsin(α-β)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网