题目内容
若函数f(x)=x2-
lnx+1在其定义域内的一个子区间(a-1,a+1)内存在极值,则实数a的取值范围 .
| 1 |
| 2 |
考点:利用导数研究函数的极值
专题:计算题,函数的性质及应用,导数的综合应用
分析:求f(x)的定义域为(0,+∞),求导f′(x)=2x-
•
=
;从而可得
∈(a-1,a+1);从而求得.
| 1 |
| 2 |
| 1 |
| x |
| 4x2-1 |
| 2x |
| 1 |
| 2 |
解答:
解:f(x)=x2-
lnx+1的定义域为(0,+∞),
f′(x)=2x-
•
=
;
∵函数f(x)=x2-
lnx+1在其定义域内的一个子区间(a-1,a+1)内存在极值,
∴f′(x)=2x-
•
=
在区间(a-1,a+1)上有零点,
而f′(x)=2x-
•
=
的零点为
;
故
∈(a-1,a+1);
故a-1<
<a+1;
解得,
<a<
;
又∵a-1≥0,
∴a≥1;
故答案为:[1,
).
| 1 |
| 2 |
f′(x)=2x-
| 1 |
| 2 |
| 1 |
| x |
| 4x2-1 |
| 2x |
∵函数f(x)=x2-
| 1 |
| 2 |
∴f′(x)=2x-
| 1 |
| 2 |
| 1 |
| x |
| 4x2-1 |
| 2x |
而f′(x)=2x-
| 1 |
| 2 |
| 1 |
| x |
| 4x2-1 |
| 2x |
| 1 |
| 2 |
故
| 1 |
| 2 |
故a-1<
| 1 |
| 2 |
解得,
| 1 |
| 2 |
| 3 |
| 2 |
又∵a-1≥0,
∴a≥1;
故答案为:[1,
| 3 |
| 2 |
点评:本题考查了导数的综合应用及函数的零点的应用,属于中档题.

练习册系列答案
相关题目
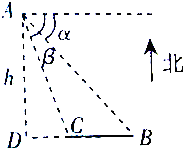 如图,从气球A测得正前方的济南全运会东荷、西柳两个场馆B、C的俯角分别为α、β,此时气球的高度为h,则两个场馆B、C间的距离为( )
如图,从气球A测得正前方的济南全运会东荷、西柳两个场馆B、C的俯角分别为α、β,此时气球的高度为h,则两个场馆B、C间的距离为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图过拋物线y2=2px(p>0)的焦点F的直线依次交拋物线及准线于点A,B,C,若|BC|=2|BF|,且|AF|=3,则拋物线的方程为( )
如图过拋物线y2=2px(p>0)的焦点F的直线依次交拋物线及准线于点A,B,C,若|BC|=2|BF|,且|AF|=3,则拋物线的方程为( )A、y2=
| ||
| B、y2=3x | ||
C、y2=
| ||
| D、y2=9x |