题目内容
给出下列四个命题:
①“x<1”是“x2<1”的充分不必要条件
②若f(x)是定义在[-1,1]的偶函数且在[-1,0]上是减函数,θ∈(
,
),则f(sinθ)<f(cosθ)
③若f(x)的图象在点A(1,f(1))处的切线方程是y=
x+2,则f(1)+f′(1)=3
④若f(x)=lg(
-x),则f(lg2)+f(lg
)=0
⑤函数f(x)=ex+x-2在区间(0,1)上有零点.
其中所有正确命题的序号是 .
①“x<1”是“x2<1”的充分不必要条件
②若f(x)是定义在[-1,1]的偶函数且在[-1,0]上是减函数,θ∈(
| π |
| 4 |
| π |
| 2 |
③若f(x)的图象在点A(1,f(1))处的切线方程是y=
| 1 |
| 2 |
④若f(x)=lg(
| x2+1 |
| 1 |
| 2 |
⑤函数f(x)=ex+x-2在区间(0,1)上有零点.
其中所有正确命题的序号是
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:①由于“-1<x<1”?“x2<1”,可得“x<1”与“x2<1”关系;
②由于f(x)是定义在[-1,1]的偶函数且在[-1,0]上是减函数,可得f(x)在[0,1]上是增函数.
由于θ∈(
,
),可得cosθ<sinθ,即可判断出;
③由f(x)的图象在点A(1,f(1))处的切线方程是y=
x+2,可得f′(1)=
,f(1)=
×1+2,即可判断出.
④函数f(x)的定义域为R,利用f(x)+f(-x)=0,f(lg
)=f(-lg2),即可判断出;
⑤利用已知可得f(0)f(1)<0.和函数零点判定定理即可判断出.
②由于f(x)是定义在[-1,1]的偶函数且在[-1,0]上是减函数,可得f(x)在[0,1]上是增函数.
由于θ∈(
| π |
| 4 |
| π |
| 2 |
③由f(x)的图象在点A(1,f(1))处的切线方程是y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
④函数f(x)的定义域为R,利用f(x)+f(-x)=0,f(lg
| 1 |
| 2 |
⑤利用已知可得f(0)f(1)<0.和函数零点判定定理即可判断出.
解答:
解:①∵“-1<x<1”?“x2<1”,∴“x<1”是“x2<1”的必要不充分条件,因此不正确;
②若f(x)是定义在[-1,1]的偶函数且在[-1,0]上是减函数,则f(x)在[0,1]上是增函数.
∵θ∈(
,
),∴0<cosθ<sinθ<1,f(sinθ)>f(cosθ),因此不正确;
③若f(x)的图象在点A(1,f(1))处的切线方程是y=
x+2,
∴f′(1)=
,f(1)=
×1+2=
.
∴f(1)+f′(1)=
+
=3,正确.
④函数f(x)的定义域为R,∵f(x)+f(-x)=lg(
-x)+lg(
+x)=lg1=0,
∴f(lg2)+f(lg
)=f(lg2)+f(-lg2)=0,正确;
⑤∵f(0)=1-2=-1,f(1)=e+1-2=e-1>0,∴f(0)f(1)<0.
∴函数f(x)=ex+x-2在区间(0,1)上有零点,正确.
综上可知:只有③④⑤正确.
故答案为:③④⑤.
②若f(x)是定义在[-1,1]的偶函数且在[-1,0]上是减函数,则f(x)在[0,1]上是增函数.
∵θ∈(
| π |
| 4 |
| π |
| 2 |
③若f(x)的图象在点A(1,f(1))处的切线方程是y=
| 1 |
| 2 |
∴f′(1)=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴f(1)+f′(1)=
| 1 |
| 2 |
| 5 |
| 2 |
④函数f(x)的定义域为R,∵f(x)+f(-x)=lg(
| x2+1 |
| x2+1 |
∴f(lg2)+f(lg
| 1 |
| 2 |
⑤∵f(0)=1-2=-1,f(1)=e+1-2=e-1>0,∴f(0)f(1)<0.
∴函数f(x)=ex+x-2在区间(0,1)上有零点,正确.
综上可知:只有③④⑤正确.
故答案为:③④⑤.
点评:本题综合考查了函数的单调性、奇偶性、函数零点判定定理、充分必要条件等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
下列说法中,正确的是( )
| A、命题“若am2<bm2,则a<b”的逆命题是真命题 |
| B、命题“p或q”为真命题,则命题“p”和命题“q”均为真命题 |
| C、命题“?x∈R,x2-x>0”的否定是:“?x∈R,x2-x≤0” |
| D、已知x∈R,则“x>1”是“x>2”的充分不必要条件 |
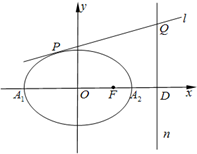 如图,已知椭圆
如图,已知椭圆 如图,椭圆C:
如图,椭圆C: