Question

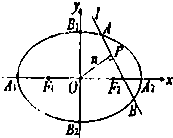
如图，椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的左、右焦点分别为F₁、F₂．椭圆上两点A、B满足：△ABF₂的周长为8，点F₁在边AB上，cos∠ABF₂=

3

5

，|BF₂|=

3

2

．
（1）求椭圆C的方程；
（2）若点P为椭圆的右顶点，直线l：y=kx+m与椭圆C交于两点M，N（M，N不是左右顶点），且

PM

⊥

PN

．试说明：直线l过定点，并求出该定点的坐标．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）由题设条件结合椭圆性质利用余弦定理推导出a=2，c²=1．由此能求出椭圆C的方程．
（2）设M（x₁，y₁），N（x₂，y₂），将y=kx+m代入椭圆方程得（4k²+3）x²+8kmx+4m²-12=0．由此利用韦达定理和向量知识能证明直线l：y=k（x-

7

2

）恒过定点（

7

2

，0）．

解答： （1）解：∵椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的左、右焦点分别为F₁、F₂，
椭圆上两点A、B满足：△ABF₂的周长为8，
点F₁在边AB上，cos∠ABF₂=

3

5

，|BF₂|=

3

2

，
∴4a=8，解得a=2，
|BF₁|=2a-

3

2

=4-

3

2

=

5

2

，
cos∠ABF₂=

( 5 2 )2+( 3 2 )2-(2c)2

2× 5 2 × 3 2

=

3

5

，解得c²=1．
∴b²=a²-c²=4-1=3，
∴椭圆C的方程为

x2

4

+

y2

3

=1．
（2）证明：设M（x₁，y₁），N（x₂，y₂），
将y=kx+m代入椭圆方程得（4k²+3）x²+8kmx+4m²-12=0．
∴x₁+x₂=

-8km

4k2+3

，x₁x₂=

4m2-12

4k2+3

，
∵y₁=kx₁+m，y₂=kx₂+m，
∴y₁y₂=k²x₁x₂+（km-2）（x₁+x₂）+m²，
∵点P为椭圆的右顶点，且

PM

⊥

PN

，
∴P（2，0），

PM

=（x₁-2，y₁），

PN

=（x₂-2，y₂），
∴

PM

•

PN

=（x₁-2）（x₂-2）+y₁y₂=0，
∴7m²+16km+4k²=0，
∴m=-

2

7

k或m=-2k都满足△＞0，
若m=-2k直线l恒过定点（2，0）不合题意舍去，
若m=-

2

7

k直线l：y=k（x-

7

2

）恒过定点（

7

2

，0）．

点评：本题考查椭圆方程的求法，考查直线恒过定点的证明，解题时要认真审题，注意函数与方程思想的合理运用．