题目内容
f(x)=kx2-3x+5在(0,+∞)上是减函数,则f(2)的范围是 .
考点:二次函数的性质
专题:函数的性质及应用
分析:由f(x)=kx2-3x+5在(0,+∞)上是减函数,求得k的取值范围,从而求得f(2)的取值范围.
解答:
解:∵f(x)=kx2-3x+5在(0,+∞)上是减函数,
当k=0时,f(x)=-3x+5满足题意;
当k>0时,f(x)=kx2-3x+5不满足题意,舍去;
当k<0时,f(x)=kx2-3x+5在-
<0时满足题意,即k<0;
∴k≤0;
∴f(2)=4k-6+5=4k-1是增函数,在k=0时取得最大值-1;
∴f(2)的取值范围是(-∞,-1];
故答案为:(-∞,-1].
当k=0时,f(x)=-3x+5满足题意;
当k>0时,f(x)=kx2-3x+5不满足题意,舍去;
当k<0时,f(x)=kx2-3x+5在-
| -3 |
| 2k |
∴k≤0;
∴f(2)=4k-6+5=4k-1是增函数,在k=0时取得最大值-1;
∴f(2)的取值范围是(-∞,-1];
故答案为:(-∞,-1].
点评:本题考查了函数的单调性及其应用问题,是中档题.

练习册系列答案
相关题目
下列表述正确的是( )
| A、0∈∅ | B、{0}∈∅ |
| C、{0}⊆∅ | D、∅⊆{0} |
已知向量
,
都是单位向量,且|
-
|=
,则
(
+
)的值为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| a |
| b |
| A、-1 | ||
B、
| ||
| C、0 | ||
| D、1 |
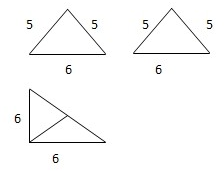 已知某三棱锥的三视图如表示,
已知某三棱锥的三视图如表示,