题目内容
请用数学归纳法证明:1+3+6+…+
=
(n∈N*)
| n(n+1) |
| 2 |
| n(n+1)(n+2) |
| 6 |
考点:数学归纳法
专题:点列、递归数列与数学归纳法
分析:根据数学归纳法的证题步骤,先证n=1时,等式成立;再假设n=k时,等式成立,再证n=k+1时等式成立.
解答:
证明:①n=1时,左边=1,右边=
=1,等式成立;
②假设n=k时,结论成立,即:1+3+6+…+
=
,
则n=k+1时,等式左边=1+3+6+…+
+
=
+
=
,
故n=k+1时,等式成立
由①②可知:1+3+6+…+
=
(n∈N*).
| 1×2×3 |
| 6 |
②假设n=k时,结论成立,即:1+3+6+…+
| k(k+1) |
| 2 |
| k(k+1)(k+2) |
| 6 |
则n=k+1时,等式左边=1+3+6+…+
| k(k+1) |
| 2 |
| (k+1)(k+2) |
| 2 |
| k(k+1)(k+2) |
| 6 |
| (k+1)(k+2) |
| 2 |
| (k+1)(k+2)(k+3) |
| 6 |
故n=k+1时,等式成立
由①②可知:1+3+6+…+
| n(n+1) |
| 2 |
| n(n+1)(n+2) |
| 6 |
点评:本题的考点是数学归纳法,主要考查数学归纳法的第二步,在假设的基础上,n=k+1时等式左边增加的项,关键是搞清n=k时,等式左边的规律,从而使问题得解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若函数y=
,当函数值y=8时,则自变量x的值是( )
|
A、±
| ||
B、-
| ||
C、±
| ||
| D、4 |
不等式
>0的解集是( )
| x-2 |
| x-3 |
| A、(2,3) |
| B、(3,+∞) |
| C、(2,+∞) |
| D、(-∞,2)(3,+∞) |
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,AB∥DC,AB⊥BC,
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,AB∥DC,AB⊥BC,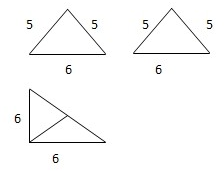 已知某三棱锥的三视图如表示,
已知某三棱锥的三视图如表示,