题目内容
设a∈R,则“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”是“a=1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:本题的关键是弄清两直线平行的等价条件,再结合充分必要条件的判断
解答:
解:必要性:设a∈R,若“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”
那么a(a+1)=2*1所以,a=1或a=-2
充分性:若a=1,
那么,直线l1:x+2y-1=0与直线l2:x+2y+4=0显然是平行的
∴设a∈R,则“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”是“a=1”的必要不充分条件、
故选B
那么a(a+1)=2*1所以,a=1或a=-2
充分性:若a=1,
那么,直线l1:x+2y-1=0与直线l2:x+2y+4=0显然是平行的
∴设a∈R,则“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”是“a=1”的必要不充分条件、
故选B
点评:判断充要条件的方法是:
①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;
②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;
③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;
④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.
①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;
②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;
③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;
④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
相关题目
经过点P(1,1)的直线在两坐标轴上的截距都是正值,若使截距之和最小,则该直线的方程为 ( )
| A、x-y=0 |
| B、x+y-2=0 |
| C、x-2y+1=0 |
| D、x+2y-3=0 |
下列表述正确的是( )
| A、0∈∅ | B、{0}∈∅ |
| C、{0}⊆∅ | D、∅⊆{0} |
若函数y=
,当函数值y=8时,则自变量x的值是( )
|
A、±
| ||
B、-
| ||
C、±
| ||
| D、4 |
已知向量
,
都是单位向量,且|
-
|=
,则
(
+
)的值为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| a |
| b |
| A、-1 | ||
B、
| ||
| C、0 | ||
| D、1 |
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,AB∥DC,AB⊥BC,
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,AB∥DC,AB⊥BC,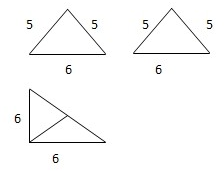 已知某三棱锥的三视图如表示,
已知某三棱锥的三视图如表示,