题目内容
已知各项均为正数的数列{an}中,a1=1,Sn是{an}的前n项和,对任意的正整数n,都有2Sn=2P
+Pan-P(P∈R)都成立,
(1)求常数P的值;
(2)求数列{an}的通项公式.
| a | 2 n |
(1)求常数P的值;
(2)求数列{an}的通项公式.
考点:数列递推式
专题:等差数列与等比数列
分析:(1)由a1=1及把n=1代入到递推公式中2Sn=2pan2+pan-p可求p
(2)由2Sn=2an2+an-1,可得2Sn-1=2an-12+an-1-1(n≥2),两式相减整理可得 (an+an-1)(2an-2an-1-1)=0,结合已知数列{an}各项均为正数可得,an-an-1=
,由等差数列的通项公式可求
(2)由2Sn=2an2+an-1,可得2Sn-1=2an-12+an-1-1(n≥2),两式相减整理可得 (an+an-1)(2an-2an-1-1)=0,结合已知数列{an}各项均为正数可得,an-an-1=
| 1 |
| 2 |
解答:
解::(1)由a1=1及2Sn=2pan2+pan-p(n∈N*),
得:2=2p+p-p
∴p=1
(2)由2Sn=2an2+an-1①
得2Sn-1=2an-12+an-1-1(n≥2,n∈N*) ②
由①-②得 2an=2(an2-an-12)+(an-an-1)
即:2(an+an-1)(an-an-1)-(an+an-1)=0∴(an+an-1)(2an-2an-1-1)=0
由于数列{an}各项均为正数
∴2an-2an-1=1即
an-an-1=
,
∴数列{an}是首项为1,公差为
的等差数列,
∴数列{an}的通项公式是an=
(n-1).
得:2=2p+p-p
∴p=1
(2)由2Sn=2an2+an-1①
得2Sn-1=2an-12+an-1-1(n≥2,n∈N*) ②
由①-②得 2an=2(an2-an-12)+(an-an-1)
即:2(an+an-1)(an-an-1)-(an+an-1)=0∴(an+an-1)(2an-2an-1-1)=0
由于数列{an}各项均为正数
∴2an-2an-1=1即
an-an-1=
| 1 |
| 2 |
∴数列{an}是首项为1,公差为
| 1 |
| 2 |
∴数列{an}的通项公式是an=
| 1 |
| 2 |
点评:本题主要考查了利用数列的递推公求解数列的通项公式,要注意对n=1的检验,及利用递推公式构造特殊(等差)数列求通项公式.

练习册系列答案
相关题目
若
=
,则tan2α=( )
| 1+cos2α |
| sin2α |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
经过点P(1,1)的直线在两坐标轴上的截距都是正值,若使截距之和最小,则该直线的方程为 ( )
| A、x-y=0 |
| B、x+y-2=0 |
| C、x-2y+1=0 |
| D、x+2y-3=0 |
设f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=4x(1-x),则f(-
)=( )
| 9 |
| 2 |
| A、1 | B、-1 | C、-63 | D、63 |
下列表述正确的是( )
| A、0∈∅ | B、{0}∈∅ |
| C、{0}⊆∅ | D、∅⊆{0} |
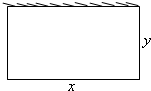 现要用一段长为l的篱笆围成一边靠墙的矩形菜园(如图所示),则围成的菜园最大面积是
现要用一段长为l的篱笆围成一边靠墙的矩形菜园(如图所示),则围成的菜园最大面积是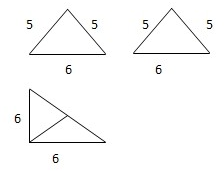 已知某三棱锥的三视图如表示,
已知某三棱锥的三视图如表示,