题目内容
已知△ABC外接圆的半径为1,圆心为O.若|
|=|
|,且2
+
+
=0,则
•
等于( )
| OA |
| AB |
| OA |
| AB |
| AC |
| CA |
| CB |
A、
| ||
B、2
| ||
C、
| ||
| D、3 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由已知2
+
+
=0,得到
+
=
,说明O为边BC的中点,得到△ABC是直角三角形,∠A为直角.再由|
|=|
|,得到△AOB为正三角形,求得角B的值,在直角三角形BAC中进一步求得角C及边AC的长,代入数量积公式求得
•
的值.
| OA |
| AB |
| AC |
| OB |
| OC |
| 0 |
| OA |
| AB |
| CA |
| CB |
解答:
解:∵2
+
+
=
,
∴
+
+
+
=
,
则
+
=
,
∴O为BC的中点,故△ABC是直角三角形,∠A为直角.
又|
|=|
|,∴△AOB为正三角形,
则∠B=60°,
在Rt△BAC中,由AB=1,BC=2,得AC=
,即
|
|=
,|
|=2,且
与
的夹角为30°,
由数量积公式可得
•
=|
||
|cos30°=
×2×
=3
故选:D.
| OA |
| AB |
| AC |
| 0 |
∴
| OA |
| AB |
| OA |
| OC |
| 0 |
则
| OB |
| OC |
| 0 |
∴O为BC的中点,故△ABC是直角三角形,∠A为直角.
又|
| OA |
| AB |
则∠B=60°,
在Rt△BAC中,由AB=1,BC=2,得AC=
| 3 |
|
| CA |
| 3 |
| CB |
| CA |
| CB |
由数量积公式可得
| CA |
| CB |
| CA |
| CB |
| 3 |
| ||
| 2 |
故选:D.
点评:本题考查了平面向量数量积的运算,考查了数学转化思想方法,在三角形ABC中,若
+
+
=
,则O为三角形ABC的外心,是中档题.
| OA |
| OB |
| OC |
| 0 |

练习册系列答案
相关题目
已知向量
,
都是单位向量,且|
-
|=
,则
(
+
)的值为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| a |
| b |
| A、-1 | ||
B、
| ||
| C、0 | ||
| D、1 |
已知空间上的两点A(-1,2,1)、B(-2,0,3),以AB为体对角线构造一个正方体,则该正方体的体积为( )
| A、3 | ||
B、2
| ||
| C、9 | ||
D、3
|
不等式
>0的解集是( )
| x-2 |
| x-3 |
| A、(2,3) |
| B、(3,+∞) |
| C、(2,+∞) |
| D、(-∞,2)(3,+∞) |
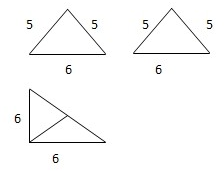 已知某三棱锥的三视图如表示,
已知某三棱锥的三视图如表示,