题目内容
平面四边形ABCD中,AD=AB=
,CD=CB=
,且AD⊥AB,现将△ABD沿着对角线BD翻折成△A′BD,则在△A′BD折起至转到平面BCD内的过程中,直线A′C与平面BCD所成的最大角的正切值为( )
| 2 |
| 5 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
考点:直线与平面所成的角
专题:空间角
分析:连结AC,BD,交于点O,由题设条件推导出OA=1,OC=2.将△ABD沿着对角线BD翻折成△A′BD,当A′C与以O为圆心,OA′为半径的圆相切时,直线A′C与平面BCD所成角最大,由此能求出结果.
解答:
解:如图,平面四边形ABCD中,
连结AC,BD,交于点O,
∵AD=AB=
,CD=CB=
,且AD⊥AB,
∴BD=
=2,AC⊥BD,
∴BO=OD=1,
∴OA=
1,OC=
=2.
将△ABD沿着对角线BD翻折成△A′BD,
当A′C与以O为圆心,OA′为半径的圆相切时,
直线A′C与平面BCD所成角最大,
此时,Rt△OA′C中,OA′=OA=1,OC=2,
∴∠OCA′=30°,
∴直线A′C与平面BCD所成的最大角为30°,其正切值为tan30°=
.
故选C.

连结AC,BD,交于点O,
∵AD=AB=
| 2 |
| 5 |
∴BD=
| 2+2 |
∴BO=OD=1,
∴OA=
(
|
(
|
将△ABD沿着对角线BD翻折成△A′BD,
当A′C与以O为圆心,OA′为半径的圆相切时,
直线A′C与平面BCD所成角最大,
此时,Rt△OA′C中,OA′=OA=1,OC=2,
∴∠OCA′=30°,
∴直线A′C与平面BCD所成的最大角为30°,其正切值为tan30°=
| ||
| 3 |
故选C.
点评:本题考查直线与平面所成角的正弦值的最大值的求法,解题要注意等价转化思想和数形结合思想的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=4x(1-x),则f(-
)=( )
| 9 |
| 2 |
| A、1 | B、-1 | C、-63 | D、63 |
已知a,b∈R且a>b,则下列不等式中成立的是( )
A、
| ||
| B、a2>b2 | ||
| C、ln(a-b)>0 | ||
| D、2a-b>1 |
已知空间上的两点A(-1,2,1)、B(-2,0,3),以AB为体对角线构造一个正方体,则该正方体的体积为( )
| A、3 | ||
B、2
| ||
| C、9 | ||
D、3
|
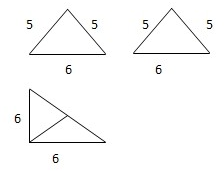 已知某三棱锥的三视图如表示,
已知某三棱锥的三视图如表示,